专题考案(3)三角板块测试

第Ⅰ卷　(选择题　共60分)

一、选择题(12×5′＝60′)

1.已知sin(α+β)=1,tanβ=,则tanα的值为　　(　　)

A.-3　　　　  B.-　　　　 C.　　　　　 D.3

2.已知,则tanα的值是　　(　　)

A.1　　  　　B.-2　　　　　 C.1或-2　　　　  D.-1或2

3.定义在R上的偶函数f (x)满足f (x+1)=-f (x)，且在［-3,-2］上是减函数，α、β是锐角三角形的两个内角，则　　(　　)

A.f (sinα)>f (cosβ)　　　　　　  B.f (sinα)<f (cosβ)

C.f (sinα)>f (sinβ)　　　　　　　 D.f (cosα)>f (cosβ)

4.函数y=Asin(ωx+φ)(ω>0,A≠0)的图象与函数y=Acos(ωx+φ)(ω>0,A≠0)的图象在区间(，)上　　(　　)

A.至少有两个交点　　　　　 B.至多有两个交点

C.至多有一个交点　　　　　 D.至少有一个交点

当sinx≥cos-x时 当sinx<cos x时

5.对于函数f (x)=　　　　　　　　　　 ，下列命题中正确的是　　(　　)

A.该函数的值域是［-1,1］

B.当且仅当x=2kπ+(k∈Z)时，函数取得最大值1

C.该函数是以π为最小正周期的周期函数

第6题图

D.当且仅当2kπ+π<x<2kπ+(k∈Z)时，f (x)<0

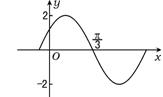
6.已知函数y=2sin(ωx+φ)(ω>0,φ<)的图象的

一部分如图所示，则ω、φ的值可能是　　(　　)

A.ω=5,φ=　　  B.ω=1,φ=-

C.ω=2,φ=　　  D.ω=3,φ=-

7.已知两线段a=2,b=2，若以a、b为边作三角形，则a边所对的角A的取值范围是　　(　　)

A.　　　 B.　　　　C.　　　　D.

8.设函数f (x)=2sin(x+),若对任意x∈R都有f ()≤f (x)≤f ()成立，则-的最小值为(　　)

A.4　　　　　 B.2　　　　  C.1 　　　　　D.

9.把函数y=sin(2x+)的图象向右平移φ(φ>0)个单位，所得的图象关于y轴对称，则φ的最小值是　　(　　)

A.　　　　 B.　　　　C.　　　　D.

10.若函数f (x)=sinωx+acosωx(ω>0)的图象关于点M (,0)对称，且在x=处函数有最小值，则a+ω的一个可能的取值是　　（　　）

A.0　　　　 B.3　　　　  C.6　　　　 D.9

11.函数y=2sinxsin2x的最大值是　　(　　)

A.　　　　B.　　　 　C.2　　　　  D.

12.已知α、β是锐角，sinα=x,cosβ=y,cos(α+β)=-,则y与x的函数关系式为（　　）

A.y=- (<x<1)

B.y=- (0<x<1)

C.y=- (0<x<)

D.y=- (0<x<1)

第Ⅱ卷　(非选择题　共90分)

二、填空题(4×4′＝16′)

13.函数y=sinx+cos()的图象中相邻两对称轴的距离是　　　　 .

14.为偶函数,则a的值是　　　　  .

15.当x≥y≥0，且3≤x+y≤5时，的最大值为　　　　　  .

16.给出下列命题：①存在实数x，使sinx+cosx=;

②若α、β是第一象限角，且α>β,则cosα<cosβ；

③函数是偶函数；

④若cosαcosβ=1，则sin(α+β)=0；

⑤将函数y=sin2x的图象向左平移个单位，得到的是函数的图象，其中正确命题的序号是　　　　　　 .

三、解答题(5×12′+14′＝74′)

17.已知函数f (x)=(a∈R)，

(1)若x∈R,求f (x)的单调递增区间.

(2)若x∈时，f (x)的最大值为4，求a的值.

18.已知函数f (x)=a+bsinx+ccosx(x∈R)的图象经过点A(0,1),B,且b>0,又f (x)的最大值为2-1.

(1)求函数f (x)的解析式；

(2)由函数y=f (x)的图象经过平移是否能得到一个奇函数y=g(x)的图象？若能，请写出平移过程；若不能，请说明理由.

19.已知函数f (x)=a+bsinx+ccosx的图象经过点A(0,1),B；当x∈［0,］时f (x)的最大值为2-1.求f (x)的解析式.

20.已知函数.

(1)设t=sinx+cosx,t为何值时，函数y取得最小值；

(2)若函数y的最小值为1,试求a的值.

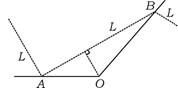
21.如图所示，某城市有一条公路从正西方AO通过市中心O后转向东北方OB，现要修建一条铁路L，L在AO上设一站A，在OB上设一站B，铁路在AB部分为直线段，现要求市中心O与AB的距离为10 km，问把A、B分别设在公路距中心O多远处才能使AB最短，并求其最短距离.

	第21题图

22.设函数f (x)的定义域为R，对任意实数α、β，有f (α)+f (β)=2f ·f,且

,.

(1)求f (0)及的值.

(2)求证：f (-x)=f (x)=-f (π-x).

(3)若0≤x<时，f (x)>0，求证:f (x)在［0,π］上单调递减.

(4)求f (x)的最小正周期.

参考答案

1.D　∵α+β=2kπ+ (k∈Z),∴tanα=tan(2kπ+-β)=tan(-β)=cotβ=,∴选D.

2.C　由

=

=1或-2.

3.A　∵f (x+1)=-f (x),且f (x)为偶函数，∴f (x)的周期为2，且关于直线x=1对称，故当x∈［-3,-2］上是减函数，则在［0，1］上是增函数.

又α+β>,α>-β,∴sinα>cosβ>0.∴f (sinα)>f (cosβ).

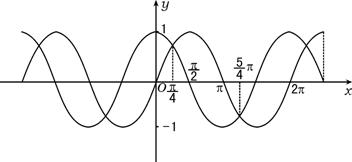
4.C　不失一般性，令ω=1,φ=0,A=1，于是两函数即为y=sinx,y=cosx，则在区间(,+π)上判断两函数图象交点的个数，如图所示.

	第4题图解

区间(,+π)长度为半个周期(不包括两端点)，显然C正确，如=，则在区间(,)内两函数图象无交点；又如0<<,则π<+π<,此时两函数图象有一个交点(横坐标为).

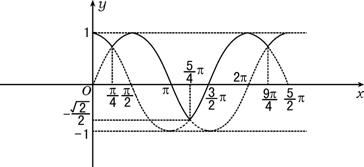
5.D　在直角坐标系内作出函数f (x)的图象(一部分)，如图实线所示.

	第5题图解

由图象知:该函数的值域为［-,1］；当函数取得最大值时，x=2kπ+(k∈Z)或x=2kπ(k∈Z)；该函数的周期为2π；当且仅当2kπ+π<x<2kπ+(k∈Z)时，f (x)<0.

6.C　从图象中可以看出，函数图象是由y=2sinωx向左平移得到，故φ>0，剔除选项B、D，再由A、C中φ=结合点(，0)是函数值由正变到负值时经过的零点，或它是“五点法”中的第三个关键点，故应有ω·+=π，即ω=2.

7.D　由a∶sinA=b∶sinB,得sinA=sinB≤,∴A∈(0,.

8.B　依题意f ()为最小值，f ()为最大值，联系f (x)的图象，-最小时为半个周期长，∴.

9.B　,由，

则(k∈Z)，此时φ无解；

或 (k∈Z),又φ>0，

故φ的最小值为.

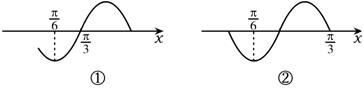
10.D　如图，下列两种情况都有可能.

	第10题图解

如图①，周期，∴ω=3.又最小值-，a=0.

但a=0时，f ()为最大值，故不可能.如图②，周期T=,ω=9,

又最小值,a=0,f ()恰为最小值.

11.B　

≤,

当且仅当时取“=”.

12.A　y=cosβ=cos［(α+β)-α］=cos(α+β)cosα+sin(α+β)sinα=-,

且.

13.　,

相邻两对称轴的距离为半个周期，即.

14.1

∴a=1时为偶函数,故填a=1.

15.25　令,，3≤r≤5，于是,

=

　　　　　　　  =

当且仅当，r=5时取得最大值25.

16.③④　由于sinx+cosx=,故不存在x，使得sinx+cosx=;

令α=，β=,则α>β,且α、β∈I,但cosα>cosβ,故②是假命题；

 =-cosx，故③为真命题；

由cosαcosβ=1，知cosα=1且cosβ=1或cosα=-1或cosβ=-1，

则sinα=sinβ=0sin(α+β)=sinαcosβ+cosαsinβ=0.故④为真命题；

将函数的图象向左平移个单位，得到的是

的图象.故⑤是假命题，综上所述，③④为真命题.

17.解　(1)f (x)=

解不等式,得(k∈Z)

∴f (x)的单调递增区间为［ (k∈Z).

(2)若0≤x≤,则≤2x+≤，则当,

即x=时，f (x)取得最大值.∴a+3=4,a=1.

18.解　(1)f (x)=,

又图象经过(0,1)、，其最大值为-1.

∴，解得,

∴f (x)=-1+2sinx+2cosx

(2)能.　f (x)=-1+sin,

把f (x)的图象向上平移1个单位，得的图象，把的图象向右平移个单位，得的图象.g(x)=sinx即为一个奇函数.

19.解　由题意知

∴f (x)=a+(1-a)(sinx+cosx)=a+(1-a)sin(x+).

∵x∈［0,］，∴.

∴当1-a>0时，a+(1-a)=2-1,a=-1.

当1-a<0时，a+(1-a)·=2-1，无解.

当1-a=0时，f (x)=a=2-1，矛盾.

综上可得，a=-1，∴f (x)=-1+2sinx+2cosx.

20.解　(1)∵t=sinx+cosx=sin,-≤t≤,

∴,sin2x=.

∴.

∵-≤t≤,∴当t=1时，函数y取得最小值.

(2)∵=1,∴a=±.

答:a的值为±.

21.解　如题图所示，设AO=a,OB=b　∵AO在正西方向，OB为东北方向.

∴∠AOB=135°.

 (当且仅当a=b时，等号成立)，

又O到AB的距离为10 km，设∠OAB=α，则∠OBA=45°-α，

∴a=,b=,ab=.

 (α=22°30′,且a=b时，等号成立)

∴.因此当a=b=时，AB最短，其最短距离为20(+1),即当A、B分别位于OA、OB上离O点km处时，能使AB最短，其最短距离为20(+1) km.

22.解　(1)∵，

，又,=0，

∴f (0)=1,.

(2)证明　f (x)+f (-x)=2 f (0)f (x),

f (x)+f (π-x)=，

又f(0)=1, =0,∴f(-x)=f (x)=-f (π-x).

(3)∵f (-x)=f (x),且0≤x<时，f (x)>0，∴-<x<时，f (x)>0.

设0≤<≤π，则f ()-f ()=f ()＋f (π-)=.

∵0≤<≤π,

∴0≤<,-<<.

∴f ()>0,f ()>0，

∴f ()>f (),

∴f (x)在［0,π］上为减函数.

(4)∵f (-x)=-f (π-x)，∴f (x)=-f (π+x), f (π+x)=-f (2π+x).

∴f (x)=f (2π+x),即2π为f (x)的一个周期,任取α∈(0,2π).

①当α∈(0,π)时，∵f (x)在［0,π］上单调递减，∴f (0)>f (α).

②当α∈(π,2π)时，2π-α∈(0,π),f (0)>f (2π-α)=f (-α)=f (α)，

总之，当α∈(0,2π)时，f (0)>f (α+0)，∴α不可能为f (x)的周期.

∴2π为f (x)的最小正周期.