(三角)
一、选择题:
1、正弦曲线y=sinx上一点P,正弦曲线的以点P为切点的切线为直线l,则直线l的倾斜角的范围是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
2、设函数![]() 图象的一条对称轴方程为
图象的一条对称轴方程为![]() , 则直线
, 则直线![]() 的倾斜角为
的倾斜角为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D.
![]()
3、函数f(x)=2sinx+3cosx—2sinx一3cosx是 ( )
A.最小正周期为2π的奇函数 B.最小正周期为2π的偶函数
c.最小正周期为π的奇函数 D.最小正周期为π的偶函数
4、在三角形ABC中“cosA+sinA=cosB+sinB”是“C=90°”的( )
(A)充分非必要条件 (B)必要非充分条件
(C)充要条件 (D)非充分非必要条件
5、已知![]() ,那么
,那么![]()
A.![]() B.
B. ![]() C.
C.
![]() D.
D.
![]()
6、函数![]() 的最小正周期是
的最小正周期是
A 2π B π C ![]() D
D ![]()
7、![]() 是正实数,函数
是正实数,函数![]() 在
在![]() 上是增函数,那么 ( )
上是增函数,那么 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8、若函数f(x)同时具有以下两个性质:①f(x)是偶函数,②对任意实数x,都有f(![]() )= f(
)= f(![]() ),则f(x)的解析式可以是
),则f(x)的解析式可以是
A.f(x)=cosx B.f(x)=cos(2x![]() ) C.f(x)=sin(4x
) C.f(x)=sin(4x![]() ) D.f(x) =cos6x
) D.f(x) =cos6x
9、把函数![]() 的图象向右平移
的图象向右平移![]() 个单位,所得图象关于y轴对称,则
个单位,所得图象关于y轴对称,则![]() 的最小正值为
( )</PGN0029A.TXT/PGN>
的最小正值为
( )</PGN0029A.TXT/PGN>
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
10、把函数![]() 的图象沿向量
的图象沿向量![]() 的方向平移后,所得的图象关于y轴对称,则m的最小值是
的方向平移后,所得的图象关于y轴对称,则m的最小值是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11、在![]() 内,使
内,使![]() 成立的
成立的![]() 的取值范围是
的取值范围是
(A)(![]() ) (B)(
) (B)(![]() ) (C)(
) (C)(![]() ) (D)(
) (D)(![]() )
)
12、已知函数![]() 图象上,相邻的一个最大值与一个最小值点恰好在
图象上,相邻的一个最大值与一个最小值点恰好在![]() 上,则f(x)最小正周期为( )
上,则f(x)最小正周期为( )
A. 1 B. 2 C. 3 D. 4
13、若α为第二象限角,则下列各式恒小于零的是 ( )
A.sinα+cosα B.tanα+sinα C.cosα-cotα D.sinα-tanα
14、为了得到函数![]() 的图象,可将函数
的图象,可将函数![]() 的图象
的图象
A.向右平移![]() 个单位
B.向左平移
个单位
B.向左平移![]() 个单位
个单位
C.向右平移![]() 个单位
D.向左平移
个单位
D.向左平移![]() 个单位
个单位
15、函数y=cosx(sinx+cosx)的最小正周期为
A
![]() B
B![]() C
C ![]() D
D
![]()
16、函数![]() ,
,![]() 的大致图像是( )
的大致图像是( )

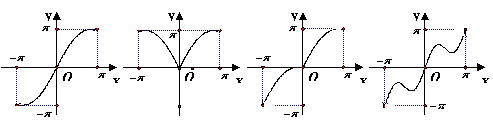
A B C D
17、.已知函数![]() 当
当![]() 时,以下结论正确的是( )
时,以下结论正确的是( )
A.
![]() B.
B.
![]()
C.
![]() D.
D.
![]()
18、如果![]() ,且
,且![]() ,那么
,那么![]()
A.
![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
19、已知sin(![]() -x)=
-x)=![]() ,则sin2x的值为( )
,则sin2x的值为( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D. ![]()
20、函数f(x)=sin(x+θ)+![]() cos(x+θ)的图像关于点(5,0)对称,则θ的值是( )
cos(x+θ)的图像关于点(5,0)对称,则θ的值是( )
A.-![]() -10
B.-
-10
B.-![]() -5 C.2kπ-
-5 C.2kπ-![]() -10 D. kπ-
-10 D. kπ-![]() -5 (k∈Z)
-5 (k∈Z)
21、要得到函数y=cos(![]() )的图像,只需将y=sin
)的图像,只需将y=sin![]() 图像( )
图像( )
A.向左平移![]() 个单位 B.向右平移
个单位 B.向右平移![]() 个单位
个单位
C.向左平移![]() 个单位 D.向右平移
个单位 D.向右平移![]() 个单位
个单位
22、已知向量![]() ,
,![]() (O为原点,
(O为原点,![]() ),则向量
),则向量![]() 的长度的最大值是( )
的长度的最大值是( )
A.![]() B.2
B.2![]() C.3
C.3![]() D.4
D.4![]()
23、曲线![]() 和直线
和直线![]() 在
在![]() 轴右侧的交点按横坐标从小到大依次记为P1,P2,P3,…,则
轴右侧的交点按横坐标从小到大依次记为P1,P2,P3,…,则![]() 等于
等于
A.![]() B.2
B.2![]()
C.3![]() D.4
D.4![]()
24
25、定义在![]() 上的函数
上的函数![]() 既是偶函数又是周期函数,若
既是偶函数又是周期函数,若![]() 的最小正周期是
的最小正周期是![]() ,且当
,且当![]() 时,
时,![]() ,则
,则![]() 的值为
的值为
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
26、已知![]() 中,
中,![]() 分别为角
分别为角![]() 所对的边,且
所对的边,且![]() ,
,![]() ,
,
![]() ,则
,则![]() 的面积为
的面积为
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
二、填空题:
曲线:![]() 的所有对称中心的坐标是
.
的所有对称中心的坐标是
.
已知函数f(x)=sin(x+![]() )+sin(x-
)+sin(x-![]() )+cosx,则函数f(x)的最小正周期为
)+cosx,则函数f(x)的最小正周期为
。
函数![]() 的最大值是
.
的最大值是
.
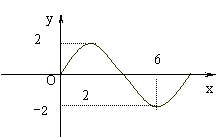 函数
函数![]() 的部分图象如图所示,则
的部分图象如图所示,则![]() _____________。
_____________。
对于函数![]() =
=![]() (
(![]() ), 则它的值域为
;
), 则它的值域为
;
已知sinα=![]() ,cos(α+β)=-
,cos(α+β)=-![]() ,α、β∈(0,
,α、β∈(0,![]() ),则sin2β的值为 。
),则sin2β的值为 。
定义运算![]() 为:
为:![]() 例如,
例如,![]() ,则函数
,则函数![]() 的值域为 .
的值域为 .

函数![]() 的减区间是
.
的减区间是
.
三、解答题:
已知函数![]() ,求:
,求:
(1)函数f(x)的定义域;
(2)函数f(x)的周期和值域.
解:(1)![]()
得![]()
(2)化简得 ![]()
所以 周期T=![]()
已知A、B、C三点的坐标分别是A(3,0),B(0,3),C(cosα,sinα),其中![]()
(1)若![]() ,求角
,求角![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的值.
的值.
已知0<x<![]() ,函数
,函数![]()
(Ⅰ)求函数f(x)的递增区间和递减区间;
(Ⅱ)若![]() ,求
,求![]() 的值。
的值。
已知点A(2,0),B(0,2),C(cos![]() ,sin
,sin![]() ),且0<
),且0<![]() <
<![]() 。
。
(1)若![]() ,求
,求![]() 与
与![]() 的夹角;
的夹角;
(2)若![]() ,求tan
,求tan![]() 的值。
的值。
解:∵(1),![]()
![]() ∴
∴![]()
又![]() ,∴
,∴![]()
又![]() ,∴
,∴![]() 与
与![]() 的夹角为
的夹角为![]() .
.![]() (5分)
(5分)
(2) ![]() ,
,![]()
∵![]() ,∴
,∴![]()
∴![]() ①
①
∴![]()
∴![]()
∵![]() ∴
∴![]()
又由![]() 及
及![]()
得![]() ②
②
由①②![]() ,
,![]()
∴![]() 。
。![]()
已知![]()
(I)求![]() ;
;
(Ⅱ)若![]() 的最小正周期及单调递减区间.
的最小正周期及单调递减区间.
解:(I)![]()
解出![]() (舍去)
(舍去)

已知A
(3,0),B
(0,3),C![]()
①若![]() =-1,求
=-1,求![]() 的值;
的值;
②若![]() ,且
,且![]() ∈(0,
∈(0,![]() ),求
),求![]() 与
与![]() 的夹角.
的夹角.
解答:(1)![]() =(
=(![]() -3,
-3,![]() ),
),![]() =(
=(![]() ,
,![]() -3),
-3),
∴由![]() ·
·![]() =-1,
=-1,
得(![]() -3)
-3)![]() +
+![]() (
(![]() -3)=-1,
……………………………2分
-3)=-1,
……………………………2分
∴![]() +
+![]() =
=![]() ,………………………………………………………4分
,………………………………………………………4分
两边平方,得1+![]() =
=![]() ,∴
,∴![]() =-
=-![]() ……………………………6分
……………………………6分
(2)![]() =(3+
=(3+![]() ,
,![]() ),
),
∴(3+![]() )2+
)2+![]() =13, ……………………………………………8分
=13, ……………………………………………8分
∴![]() =
=![]() ,∵
,∵![]() ∈(0,π),
∈(0,π),
∴![]() =
=![]() ,
,![]() =
=![]() , …………………………………………………9分
, …………………………………………………9分
∴![]() ,
,
设![]() 与
与![]() 的夹角为
的夹角为![]() ,则
,则
![]() =
=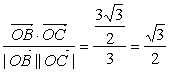 , …………………………………11分
, …………………………………11分
∴ ![]() =
=![]() 即为所求. ………………………………………………………12分
即为所求. ………………………………………………………12分
![]() 已知:
已知:
(Ⅰ)![]()
(Ⅱ)![]()
解:![]() ……3分
……3分
(Ⅰ)最小正周![]() ……6分
……6分
(Ⅱ)![]() ……9分
……9分
即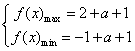
![]() 即:
即:![]()
设![]()
(1)求A、B、C的值;
(2)求![]() 的最小正周期、最小值及取得最小值时的x的值。
的最小正周期、最小值及取得最小值时的x的值。
已知向量![]() ,
,![]() .
.
(Ⅰ)当![]() ,且
,且![]() 时,求
时,求![]() 的值;
的值;
(Ⅱ)当![]() ,且
,且![]() ∥
∥![]() 时,求
时,求![]() 的值.
的值.
已知向量![]() ,
,![]() .
.
(Ⅰ)当![]() ,且
,且![]() 时,求
时,求![]() 的值;
的值;
(Ⅱ)当![]() ,且
,且![]() ∥
∥![]() 时,求
时,求![]() 的值.
的值.
解:(Ⅰ)当![]() 时,
时,![]() ,
,
![]()
![]() ,
, ![]() 由
由![]() , 得
, 得![]() , ……………………3分
, ……………………3分
上式两边平方得![]() ,
,
因此,![]() . ……………………………………………………………6分
. ……………………………………………………………6分
(Ⅱ)当![]() 时,
时,![]() ,
,
由![]() ∥
∥![]() 得
得![]() .即
.即![]() .
………………………………9分
.
………………………………9分
![]() ,
,
![]()
![]() 或
或 ![]() .
………………………………………………
.
………………………………………………
已知向量![]() .
.
(1)求函数![]() 的最小正周期;(2)求函数
的最小正周期;(2)求函数![]() 的单调减区间;
的单调减区间;
|
![]()
| |||||||||||||||||||||
|
| |||||||||||||||||||||
|
|
|
| |||||||||||||||||||
|
|
| ||||||||||||||||||||
|
| |||||||||||||||||||||
.解:![]()
![]() ………………………………5分
………………………………5分
(1)![]() ……………………………………6分
……………………………………6分
(2)![]()
![]()
|
|
从图象上可以直观看出,此函数有一个对称中心(![]() ),无对称轴…………14分
),无对称轴…………14分

