高考文科数学第四次月考试卷
注意事项:
1.答选择题前,考生务必将自己的姓名、班级、座号写在答题卡上。
2.选择填空题答案写在答题卡上。
3.主观题请在规定区域答题。请务必保持答题纸的整洁,考试结束,将答题卡交回。
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.把答案填写在答题卡相应位置上.
1.
设全集为![]() ,集合
,集合![]() ,则 ( )
,则 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.
若奇函数![]() (
(![]() )满足
)满足![]() ,则
,则![]() ( )
( )
A.0 B.1 C.![]() D.
D.![]()
3.
已知直线![]() 与直线
与直线![]() 互相垂直,则实数
互相垂直,则实数![]() 为 ( )
为 ( )
A.![]() B.0或2
C.2
D.0或
B.0或2
C.2
D.0或![]()
4.
下列函数中,最小正周期为![]() ,且图象关于直线
,且图象关于直线![]() 对称的是 ( )
对称的是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
5.
已知向量![]() ,若
,若![]()
![]() 与
与![]() 垂直,则
垂直,则![]() 等于 ( )
等于 ( )
A . ![]() B . 0
C . 1
D . 2
B . 0
C . 1
D . 2
6.
甲、乙、丙3位同学选修课程,从4门课程中,甲选修2门,乙、丙各选修3门,则不同的选修方案共有( )
A.36种
B.48种
C.96种
D.192种
7.
焦点为![]() ,且与双曲线
,且与双曲线![]() 有相同的渐近线的双曲线方程是 ( )
有相同的渐近线的双曲线方程是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.
对于R上可导的任意函数f(x),若满足![]() 则必有
则必有
A.![]() B.
B.![]()
C.![]() D.
D.![]()
9.
设![]() 是公差为正数的等差数列,若
是公差为正数的等差数列,若![]() ,
,![]() ,则
,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10. 球面上有三点A、B、C,任意两点之间的球面距离都等于球大圆周长的四分之一,且过这三点的截面圆的面积为![]() ,则此球的体积为
( )
,则此球的体积为
( )
A. ![]() B.
B. ![]() C.
C.
![]() D.
D.
![]()
11. 若![]() 展开式中各项系数之和为214,则展开式中含x2的项是( )
展开式中各项系数之和为214,则展开式中含x2的项是( )
A.第3项 B.第5项 C.第4项 D.不存在
12.
对于使![]() 成立的所有常数M中,我们把M的最小值
成立的所有常数M中,我们把M的最小值![]() 叫做
叫做![]() 的上确界,若
的上确界,若![]() ,则
,则![]() 的上确界为 ( )
的上确界为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题:本大题共4小题,每小题4分,共16分.把答案填写在答题卡相应位置上.
13.
过椭圆![]() 作直线交椭圆于A、B二点,F2是此椭圆的另一焦点,则
作直线交椭圆于A、B二点,F2是此椭圆的另一焦点,则![]() 的周长为 .
的周长为 .
14.
已知函数![]() .
.
15.
已知 ,则z的最小值为
.
,则z的最小值为
.
16. 设x,y,z是空间中不同的直线或不同的平面,且直线不在平面内,则下列结论中能保证“x⊥z,且y⊥z ,则 x//y ”为真命题的是______________________(请把你认为所有正确的结论的代号都填上).
①x为直线,y, z为平面; ②x , y , z为平面;
③x , y为直线,z为平面;
④x , y , z为直线;
⑤x , y为平面,z为直线.
三、解答题:本大题共6小题,共74分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
17.
(本小题满分12分)已知函数![]() 的定义域为
的定义域为![]() ,
,
(1)求函数的定义域![]() ;
;
(2)当![]() 时,求
时,求![]() 的最小值.
的最小值.
18.
(本题12分)已知![]() ,
,![]() .
.
(1)求![]() 的解析式及周期
的解析式及周期![]() ;
;
(2)当![]() 时,
时, ![]() ,求
,求![]() 的值.
的值.

19. 如图,正三棱柱ABC—A1B1C1中,D是BC的中点,AA1=AB=1.
(I)求证:A1C//平面AB1D;
(II)求二面角B—AB1—D的大小;
20.
(本小题满分12分)已知等差数列![]() 的公差
的公差![]() 大于0,且
大于0,且![]() 、
、![]() 是方程
是方程![]() 的两根,数列
的两根,数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]()
![]() 。
。
(1)求数列![]() 、
、![]() 的通项公式;
的通项公式;
(2)记![]() ,求证:
,求证:![]() .
.
21.
(本小题满分12分)已知函数![]() ,
,
(1)若函数![]() 的图象在点
的图象在点![]() 处的切线与直线
处的切线与直线![]() 平行,函数
平行,函数![]() 在
在![]() 处取得极值,求函数
处取得极值,求函数![]() 的解析式,并确定函数的单调递减区间;
的解析式,并确定函数的单调递减区间;
(2)若![]() ,且函数
,且函数![]() 在
在![]() 上是减函数,求
上是减函数,求![]() 的取值范围.
的取值范围.
22. (本小题满分14分)
已知椭圆![]() 过点
过点![]() ,且离心率
,且离心率![]() 。
。
(Ⅰ)求椭圆方程;
(Ⅱ)若直线![]() 与椭圆交于不同的两点
与椭圆交于不同的两点![]() 、
、![]() ,且线段
,且线段![]() 的垂直平分线过定点
的垂直平分线过定点![]() ,求
,求![]() 的取值范围。
的取值范围。
参考答案
一、选择题:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | B | B | B | C | C | B | C | B | D | C | B |
二、填空题:
13、24
14、![]() 15、-6
16、①③⑤
15、-6
16、①③⑤
三、解答题:
17、解 :(1)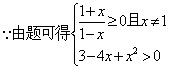
![]() (…………5分)
(…………5分)
(2)![]() (…………………6分)
(…………………6分)
又![]() ,
(…………………8分)
,
(…………………8分)
![]() (…………………10分)
(…………………10分)
故![]() (…………………12分)
(…………………12分)
18、解: (1)![]() ……3分
……3分
![]() ……………………………………………5分
……………………………………………5分
(2)![]() 时,
时, ![]() ……………………………………6分
……………………………………6分
![]() ………………………………8分
………………………………8分
![]()
![]() ………… ………………………………10分
………… ………………………………10分
![]()
![]() ………………………………………………………12分
………………………………………………………12分
19、解:解法一(I)证明:连接A1B,设A1B∩AB1 = E,连接DE.
∵ABC—A1B1C1是正三棱柱,且AA1 = AB,
∴四边形A1ABB1是正方形,
∴E是A1B的中点,又D是BC的中点, ∴DE∥A1C. ……………… 4分
∵DE![]() 平面AB1D,A1C
平面AB1D,A1C![]() 平面AB1D, ∴A1C∥平面AB1D.
…………6分
平面AB1D, ∴A1C∥平面AB1D.
…………6分
(II)解:在面ABC内作DF⊥AB于点F,在面A1ABB1内作FG⊥AB1于点G,连接DG.
∵平面A1ABB1⊥平面ABC, ∴DF⊥平面A1ABB1,
∴FG是DG在平面A1ABB1上的射影, ∵FG⊥AB1, ∴DG⊥AB1
∴∠FGD是二面角B—AB1—D的平面角 …………………………8分
设A1A = AB = 1,在正△ABC中,DF=![]()
在△ABE中,![]() , 在Rt△DFG中,
, 在Rt△DFG中,![]() ,
,
 所以,二面角B—AB1—D的大小为
所以,二面角B—AB1—D的大小为![]() …………………………12分
…………………………12分
解法二:
建立空间直角坐标系D—xyz,如图,
(I)证明:
连接A1B,设A1B∩AB1 = E,连接DE.
设A1A = AB = 1,
则![]()
![]()
![]() …………………………4分
…………………………4分
![]() ,
,
![]() ……………………………………6分
……………………………………6分
(II)解:![]() ,
, ![]() ,
,
设![]() 是平面AB1D的法向量,则
是平面AB1D的法向量,则![]() ,
,
故![]() ;
;
同理,可求得平面AB1B的法向量是![]() ……………………8分
……………………8分
设二面角B—AB1—D的大小为θ,![]() ,
,
∴二面角B—AB1—D的大小为![]() …………………………12分
…………………………12分
20、解:(1)由![]() +
+![]() =12,
=12,![]()
![]() =27,且
=27,且![]() >0,所以
>0,所以![]() =3,
=3,![]() =9,
=9,
从而![]() ,
,![]() (n∈N*)(………………………4分)
(n∈N*)(………………………4分)
在已知![]() 中,令n=1,得
中,令n=1,得![]()
当![]() 时,
时,![]() ,
,![]() ,两式相减得,
,两式相减得,![]() ,
,
![]() ,
,![]() 。(n∈N*)(………………………8分)
。(n∈N*)(………………………8分)
(2)![]()
![]() ,
,
![]()
![]()
![]() 。(………………………12分)
。(………………………12分)
21、解:(1)已知函数![]() ,
,
![]() (…………2分)
(…………2分)
又函数![]() 图象在点
图象在点![]() 处的切线与直线
处的切线与直线![]() 平行,且函数
平行,且函数![]() 在
在![]() 处取得极值,
处取得极值,![]() ,且
,且![]() ,解得
,解得![]()
![]() ,且
,且![]() (………………………6分)
(………………………6分)
令![]()
![]()
![]() ,
,
所以函数的单调递减区间为![]() (………………………8分)
(………………………8分)
(2)当![]() 时,
时,![]() ,又函数
,又函数![]() 在
在![]() 上是减函数
上是减函数
![]() 在
在![]() 上恒成立,
(………………………10分)
上恒成立,
(………………………10分)
即![]() 在
在![]() 上恒成立
上恒成立![]() 。
(………………………12分)
。
(………………………12分)
22.由题意椭圆的离心率
![]()
![]()
![]()
∴椭圆方程为![]() ……2分
……2分
又点![]() 在椭圆上
在椭圆上 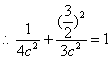
![]()
∴椭圆的方程为![]() ……4分
……4分
(Ⅱ)设![]() 由
由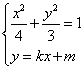
消去![]() 并整理得
并整理得![]() ……6分
……6分
∵直线![]() 与椭圆有两个交点
与椭圆有两个交点
![]() ,即
,即![]() ……8分
……8分
又![]()
![]() 中点
中点![]() 的坐标为
的坐标为![]() ……10分
……10分
设![]() 的垂直平分线
的垂直平分线![]() 方程:
方程:![]()
![]() 在
在![]() 上
上 ![]() 即
即![]()
![]() ……12分
……12分
将上式代入得![]()
![]()
即![]() 或
或![]()
![]() 的取值范围为
的取值范围为![]() ……14分
……14分
