高考理科数学摸底考试
本试卷分选择题题(8道),填空题(6道),解答题(6道)共20题。满分150分,考试时间120分钟。
一、选择题(共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的,请将正确选项填在答卷相应的位置上)
1.若![]() ,则
,则
![]() 一定不属于的区间是 ( )
一定不属于的区间是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D. ![]()
2.等差数列{an} 中,a3 =2,则该数列的前5项的和为( )
A.10 B.16 C. 20 D.32
3.设![]() 表示平面,
表示平面,![]() 表示直线,给定下列四个命题:①
表示直线,给定下列四个命题:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .
.
其中正确命题的个数有( )
A.1个 B.2个 C.3个 D.4个
4.如图,一个空间几何体的正视图、侧视图、俯视图为全等的等腰直角三角形,如果直角三角形的直角边长为1,那么这个几何体的体积为( )
A.1 B.![]() C.
C.![]() D.
D.![]()

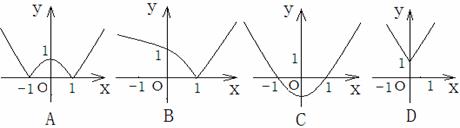 5.已知函数
5.已知函数![]() ,则函数
,则函数![]() 的图像可能是( )
的图像可能是( )
6.某班委会由4名男生与3名女生组成,现从中选出2人担任班长,其中至少有1名女生当选的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
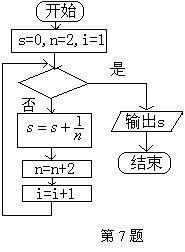 7.右图给出的是计算
7.右图给出的是计算![]() 的值的一个程序框图,其中判断框内应填入的条件是( )
的值的一个程序框图,其中判断框内应填入的条件是( )
A.i>10 B.i<10 C.i>20 D.i<20
8.定义两种运算:![]()
![]() ,
,![]() ,则函数
,则函数![]() 为( )
为( )
A.奇函数 B.偶函数
C.奇函数且为偶函数 D.非奇函数且非偶函数
二.填空题(本大题共6小题,每小题5分,共30分。请将正确答案填在答卷相应的位置上)
9.在极坐标系中,O是极点,![]() ,
,![]() 则△AOB的形状为 .
则△AOB的形状为 .
10.在![]() 中,
中,![]() 的面积为
的面积为![]() ,则
,则![]() 的值为 .
的值为 .
11.已知![]() 、
、![]() ,则不等式组
,则不等式组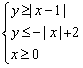 所表示的平面区域的面积是 .
所表示的平面区域的面积是 .
12.![]() 的展开式中
的展开式中![]() 项的系数是 .(用数字作答)
项的系数是 .(用数字作答)
13.F1、F2是椭圆![]()
![]() 的左、右两焦点,P为椭圆的一个顶点,若△PF1F2是等边三角形,则a2= .
的左、右两焦点,P为椭圆的一个顶点,若△PF1F2是等边三角形,则a2= .
14.若![]() ,且
,且![]() ,则
,则![]() 的值是 .
的值是 .
三.解答题(本大题共6小题,共80分.)
15.(本题满分12分)设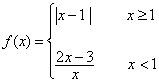 ,解不等式
,解不等式![]() .
.
16.(本题满分12分)长方体![]() 中,
中,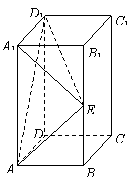
![]() ,
,![]() ,
,![]() 是侧棱
是侧棱![]() 的中点.
的中点.
(1) 求证:直线![]() 平面
平面![]() ;
;
(2) 求三棱锥![]() 的体积;
的体积;
(3)求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
17.(本题满分14分)知函数![]() (
(![]() 周期为
周期为![]() .
.
求:当![]() 时
时![]() 的取值范围.
的取值范围.
18.(本题满分14分)已知数列![]() 的前n项和
的前n项和![]() .
.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)设![]() ,求数列
,求数列![]() 的前n项和.
的前n项和.
19.(本题满分14分) 已知实数![]() 有极大值32.
有极大值32.
(1)求函数![]() 的单调区间;
的单调区间;
(2)求实数![]() 的值.
的值.
20.(本题满分14分)已知焦点在x轴上的双曲线C的两条渐近线过坐标原点,且两条渐近线与以点![]() 为圆心,1为半径为圆相切,又知C的一个焦点与A关于直线y=x对称.
为圆心,1为半径为圆相切,又知C的一个焦点与A关于直线y=x对称.
(1)求双曲线C的方程;
(2)若Q是双曲线C上的任一点,F1、F2为双曲线C的左、右两个焦点,从F1引∠F1QF2的平分线的垂线,垂足为N,试求点N的轨迹方程.
(3)设直线y=mx+1与双曲线C的左支交于A、B两点,另一直线L经过M(-2,0)及AB的中点,求直线L在y轴上的截距b的取值范围.
数学参考答案及评分标准
一、选择题:每小题5分,共50分。
CABDA CAA
二、填空题:每小题5分,共20分。
9.等腰直角三角形; 10.2; 11.![]() ;12.165
13.12 14.11
;12.165
13.12 14.11
三、解答题:共80分。
15.解:(1)当![]() 时,原不等式等价于
时,原不等式等价于![]() ,即
,即![]() 或
或![]() ……3分
……3分
∴![]() . …………………………………………………………………5分
. …………………………………………………………………5分
(2)当![]() 时,原不等式等价于
时,原不等式等价于![]() ,即
,即![]() 或
或![]() …………8分
…………8分
∴![]() . …………………………………………………………………10分
. …………………………………………………………………10分
综上所述,不等式![]() 的解集为
的解集为![]() . ………………12分
. ………………12分
16.解:(1)依题意:![]() ,
,![]() ,…………………………………2分
,…………………………………2分
则![]() 平面
平面![]() .……………………………………………………………………………3分
.……………………………………………………………………………3分
(2)![]() …………………3分(写出公式得2分,计算1分)
…………………3分(写出公式得2分,计算1分)
(3)方法一:向量法
以D为原点,DA、DC、DD1分别x轴、y轴、z轴建立空间直角坐标系,则
A(1,0,0),A1(1,0,2),D1(0,0,2),E(1,1,1)
∴![]() ……………………………………………………………5分
……………………………………………………………5分
设平面AD1E的法向量为![]()
![]() ,即
,即![]()
令![]() ,则
,则![]() ……………………………………………………………………7分
……………………………………………………………………7分
又![]() 是平面AA1D的法向量,则 ………………………………………8分
是平面AA1D的法向量,则 ………………………………………8分
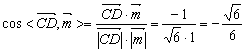 ,…………………………………………10分
,…………………………………………10分
而二面角![]() 为锐二面角,故其余弦值为
为锐二面角,故其余弦值为![]() ………………………………12分
………………………………12分
方法二:传统法(供参考)
取![]() 的中点
的中点![]() ,连
,连![]() ,则
,则![]() 、
、![]() ,
,
所以![]() 平面
平面![]() .过
.过![]() 在平面
在平面![]()
中作![]() ,交
,交![]() 于
于![]() ,连
,连![]() ,则
,则![]() ,
,
所以![]() 为二面角
为二面角![]() 的平面角
的平面角
.在![]() 中,
中,![]()
![]()
所以![]()
![]() 。
。
17.解:![]() ……………… 4分(每个公式的应用得2分)
……………… 4分(每个公式的应用得2分)
![]()
![]() …………………………………………………………
6分
…………………………………………………………
6分
因为![]() ,所以
,所以![]() ………………………………………………………… 8分
………………………………………………………… 8分
![]() ………………………………………………………… 9分
………………………………………………………… 9分
因为![]() ,所以
,所以![]() ………………………………………………… 10分
………………………………………………… 10分
![]() ……………………………………………………… 12分
……………………………………………………… 12分
故 ![]() ………………………………………………………………
14分
………………………………………………………………
14分
18.(Ⅰ)当![]() 时,
时,![]() ………………………………………………2分
………………………………………………2分
![]() 故
故![]() ,………………………………………5分
,………………………………………5分
即数列的通项公式为
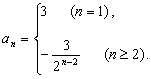 …………………………………………………… 7分
…………………………………………………… 7分
(Ⅱ)当![]() 时,
时,![]() …………………………………………………………8分
…………………………………………………………8分
当![]() ………………………………………9分
………………………………………9分
故![]() ………………………………………………………10分
………………………………………………………10分
![]() ……………………12分
……………………12分
由此可知,数列![]() 的前n项和
的前n项和![]() 为
为  ………
14分
………
14分
19.解:(1)![]()
![]() ……………………………………………3分
……………………………………………3分
令![]()
![]() ………………………………………………………4分
………………………………………………………4分
![]() ……………………………………………………………………5分
……………………………………………………………………5分
![]() …………………………………7分
…………………………………7分
∴函数![]() 的单调递增区间为
的单调递增区间为![]()
∴函数![]() 的单调递减区间为
的单调递减区间为![]() …………………………………………………9分
…………………………………………………9分
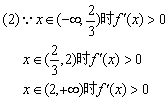
![]() 时,取得极大值……………………………………………………11分
时,取得极大值……………………………………………………11分
即 ![]()
解得 a=27 …………………………………………………………………………14分
20.解:(1)设双曲线C的渐近线方程为y=kx,即kx-y=0
∵该直线与圆 ![]() 相切,
相切,
∴双曲线C的两条渐近线方程为![]() ……………………………………………2分
……………………………………………2分
故设双曲线C的方程为![]() ,又∵双曲线C的一个焦点为
,又∵双曲线C的一个焦点为![]()
∴![]() ,∴双曲线C的方程为
,∴双曲线C的方程为![]() ………………………4分
………………………4分
(2)若Q在双曲线的右支上,则延长QF2到T,使QT=OF1
若Q在双曲线的左支上,则在QF2上取一点T,使QT=QF1
根据双曲线的定义TF2=2,所以点T在以F2![]() 为圆心,2为半径的圆上,即点T的轨迹方程是
为圆心,2为半径的圆上,即点T的轨迹方程是![]() ① ………………………………………6分
① ………………………………………6分
由于点N是线段F1T的中点,设N(x,y),T(![]() )
)
则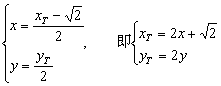
代入①并整理得点N的轨迹方程为 ![]() …………………8分
…………………8分
(3)由![]()
令![]()
直线与双曲线左支交于两点,等价于方程 ![]() 上有两个不等实根.
上有两个不等实根.
因此 ………………………………………10分
………………………………………10分
又AB中点为![]()
∴直线L的方程为![]() ………………………………12分
………………………………12分
令x=0,得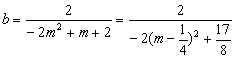
∵![]() ∴
∴![]()
∴故b的取值范围是![]() …………………………………………14分
…………………………………………14分