圆锥曲线(四) ----(圆锥曲线的应用)
班级_________ 姓名__________
1.1998年12月19日,太原卫星发射中心为摩托罗拉公司(美国)发射了两颗“铱星”系统通信卫星.卫星运行的轨道是以地球中心为一个焦点的椭圆,近地点为m km,远地点为 n km,地球的半径为R km,则通信卫星运行轨道的短轴长等于
A.2![]() B.
B. ![]() C.2mn D.mn
C.2mn D.mn
|
A.2.5 m B.4 m
C.5 m D.6 m
3.一个酒杯的轴截面是抛物线的一部分,它的方程是x2=2y(0≤y≤20).在杯内放入一个玻璃球,要使球触及酒杯底部,则玻璃球的半径r的范围为____________.
4.河上有一抛物线型拱桥,当水面距拱顶5 m时,水面宽为8 m,一小船宽4 m,高2 m,载货后船露出水面上的部分高![]() m,问水面上涨到与抛物线拱顶相距___________m时,小船不能通航.
m,问水面上涨到与抛物线拱顶相距___________m时,小船不能通航.
5. 下图是一种加热水和食物的太阳灶,上面装有可旋转的抛物面形的反光镜,镜的轴截面是抛物线的一部分,盛水和食物的容器放在抛物线的焦点处,容器由若干根等长的铁筋焊接在一起的架子支撑
下图是一种加热水和食物的太阳灶,上面装有可旋转的抛物面形的反光镜,镜的轴截面是抛物线的一部分,盛水和食物的容器放在抛物线的焦点处,容器由若干根等长的铁筋焊接在一起的架子支撑![]() 已知镜口圆的直径为12 m,镜深2 m..
已知镜口圆的直径为12 m,镜深2 m..
(1)建立适当的坐标系,求抛物线的方程和焦点的位置;
(2)若把盛水和食物的容器近似地看作点,试求每根铁筋的长度![]()
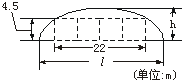
6.如下图,某隧道设计为双向四车道,车道总宽22 m,要求通行车辆限高4.5 m,隧道全长2.5 km,隧道的拱线近似地看成半个椭圆形状
(1)若最大拱高h为6 m,则隧道设计的拱宽l是多少?
(2)若最大拱高h不小于6 m,则应如何设计拱高h和拱宽l,才能使半个椭圆形隧道的土方工程量最小?
|
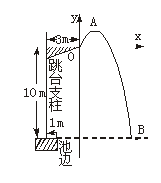
7.中国跳水运动员进行10 m跳台跳水训练时,身体(看成一点)在空中的运动路线为如下图所示坐标系下经过原点O的一条抛物线(图中标出的数据为已知条件).
在跳某个规定动作时,正常情况下,该运动员在空中的最高处距水面![]() m,入水处距池边的距离为4 m,同时,运动员在距水面高度为5 m或5 m以上时,必须完成规定的翻腾动作,并调整好入水姿势,否则就会出现失误.
m,入水处距池边的距离为4 m,同时,运动员在距水面高度为5 m或5 m以上时,必须完成规定的翻腾动作,并调整好入水姿势,否则就会出现失误.
(1)求这条抛物线的解析式;
(2)在某次试跳中,测得运动员在空中的运动路线是(1)中的抛物线,且运动员在空中调整好入水姿势时,距池边的水平距离为3![]() m,问此次跳水会不会失误?并通过计算说明理由;
m,问此次跳水会不会失误?并通过计算说明理由;
 (3)要使此次跳水不至于失误,该运动员按(1)中抛物线运行,且运动员在空中调整好入水姿势时,距池边的水平距离至多应为多少?
(3)要使此次跳水不至于失误,该运动员按(1)中抛物线运行,且运动员在空中调整好入水姿势时,距池边的水平距离至多应为多少?
8.(2006上海春)学校科技小组在计算机上模拟航天器变轨返回试验.设计方案如图:航天器运行(按顺时针方向)的轨迹方程为![]() ,变轨(即航天器运行轨迹由椭圆变为抛物线)后返回的轨迹是以
,变轨(即航天器运行轨迹由椭圆变为抛物线)后返回的轨迹是以![]() 轴为对称轴、
轴为对称轴、![]() 为顶点的抛物线的实线部分,降落点为
为顶点的抛物线的实线部分,降落点为![]() . 观测点
. 观测点![]() 同时跟踪航天器.
同时跟踪航天器.
(1)求航天器变轨后的运行轨迹所在的曲线方程;
 (2)试问:当航天器在
(2)试问:当航天器在![]() 轴上方时,观测点
轴上方时,观测点![]() 测得离航天器的距离分别为多少时,应向航天器发出变轨指令?
测得离航天器的距离分别为多少时,应向航天器发出变轨指令?
AC 3、![]() 4、
4、![]()
5、解:(1)如下图,在反光镜的轴截面内建立直角坐标系,使反光镜的顶点(即抛物线的顶点)与原点重合,x轴垂直于镜口直径.
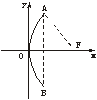
由已知,得A点坐标是(2,6),
设抛物线方程为y2=2px(p>0),
则36=2p×2,p=9.
所以所求抛物线的标准方程是y2=18x,
焦点坐标是F(![]() ,0).
,0).
(2)∵盛水的容器在焦点处,∴A、F两点间的距离即为每根铁筋长.
AF=![]() =
=![]() (或AF=
(或AF=![]() +2=
+2=![]() ).
).
故每根铁筋的长度是6.5 m.
6、(1)解:如下图建立直角坐标系,则点P(11,4![]() 5),
5),
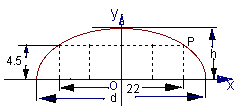 椭圆方程为
椭圆方程为![]() +
+![]() =1
=1![]()
将b=h=6与点P坐标代入椭圆方程,得
a=![]() ,此时l=2a=
,此时l=2a=![]() ≈33
≈33![]() 3
3![]()
因此隧道的拱宽约为33![]() 3 m
3 m![]()
(2)解法一:由椭圆方程![]() +
+![]() =1,得
=1,得![]() +
+![]() =1
=1![]()
因为![]() +
+![]() ≥
≥![]() ,
,
即ab≥99,且l=2a,h=b,所以S=![]() lh=
lh=![]() ≥
≥![]()
![]()
当S取最小值时,有![]() =
=![]() =
=![]() ,
,
得a=11![]() ,b=
,b=![]()
![]()
此时l=2a=22![]() ≈31
≈31![]() 1,h=b≈6
1,h=b≈6![]() 4
4![]()
故当拱高约为6![]() 4 m、拱宽约为31
4 m、拱宽约为31![]() 1 m时,土方工程量最小
1 m时,土方工程量最小![]()
解法二:由椭圆方程![]() +
+![]() =1,得
=1,得![]() +
+![]() =1
=1![]()
于是b2=![]() ·
·![]()
![]()
a2b2=![]() (a2-121+
(a2-121+![]() +242)≥
+242)≥![]() (2
(2![]() +242)=81×121,
+242)=81×121,
即ab≥99,当S取最小值时,
有a2-121=![]()
![]()
得a=11![]() ,b=
,b=![]() ,以下同解法一
,以下同解法一![]()
7、解:(1)在给定的直角坐标系下,设最高点为A,入水点为B,抛物线的解析式为
y=ax2+bx+c![]()
由题意知,O、B两点的坐标依次为(0,0)、(2,-10),且顶点A的纵坐标为![]() ,所以有c=0,
,所以有c=0,![]() =
=![]() ,4a+2b+c=-10
,4a+2b+c=-10![]()
解之得a=-![]() , b=
, b=![]() ,c=0或a=-
,c=0或a=-![]() ,b=-2,c=0
,b=-2,c=0![]()
∵抛物线对称轴在y轴右侧,∴-![]() >0
>0![]()
又∵抛物线开口向下,∴a<0![]()
∴b>0,后一组解舍去![]()
∴a=-![]() ,b=
,b=![]() ,c=0
,c=0![]()
∴抛物线的解析式为y=-![]() x2+
x2+![]() x
x![]()
(2)当运动员在空中距池边的水平距离为3![]() m时,即x=3
m时,即x=3![]() -2=
-2=![]() 时,
时,
y=(-![]() )×(
)×(![]() )2+
)2+![]() ×
×![]() =-
=-![]() ,
,
∴此时运动员距水面的高为
10-![]() =
=![]() <5
<5![]()
因此,此次跳水会出现失误![]()
(3)当运动员在x轴上方,即y>0的区域内完成动作并做好入水姿势时,当然不会失误,但很难做到![]()
∴当y<0时,要使跳水不出现失误,
则应有y≤10-5,即-y≤5![]()
∴有![]() x2-
x2-![]() x≤5,
x≤5,
解得2-![]() ≤x≤2+
≤x≤2+![]()
![]()
∴运动员此时距池边的距离至多为2+2+![]() =4+
=4+![]() m
m![]()
8、解:(1)由题意,设曲线方程为![]() , 将点D(8,0)的坐标代入,得
, 将点D(8,0)的坐标代入,得 ![]() .
. ![]() . ∴ 曲线方程为
. ∴ 曲线方程为![]() .
.
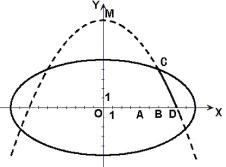 (2)设变轨点为C(x,y),根据题意可知
(2)设变轨点为C(x,y),根据题意可知
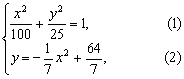
得4y2-7y-36=0,
解出y=4或y=-9/4(不合题意,舍去),
从而y=4,于是x=6或x=-6(不合题意,舍去),所以 C 点的坐标为(6,4).
应用两点之间距离公式计算,得 ![]() .
.
答:当观测点A、B测得AC、BC距离分别为 ![]() 时,应向航天器发出变轨指令.
时,应向航天器发出变轨指令.