专题考案(2)数列板块 第1课 数列的概念和运算
(时间：90分钟 满分：100分)
题型示例
写出下面数列{an}的前5项:
(1)a1=5,an=an-1+3(n≥2);
(2)a1=1,an=an-1+
(n≥2);
(3)a1=1,a2=1,an=an-1+an-2(n≥3).
分析 运用递推公式的定义解题.
解 (1)5,8,11,14,17;(2)1,2,
,
,
;(3)1,1,2,3,5.
点评 递推公式揭示一个数列相邻的两项或n项之间的关系，解题时应注意充分挖掘和发现这种关系的特征.
一、选择题(7×4′＝28′)
1．下列说法正确的是 ( )
A．数列｛an｝是等比数列的充要条件是an+1=anq(n∈N)
B．数列a、b、c是等比数列的充要条件是b2＝ac且abc≠0
C．等比数列｛an｝，当q>1时，是递增数列
D．任何两个实数都有等比中项
2．已知等差数列{an}的公差为2,若a1,a3,a4成等比数列，则a2等于 ( )
A.-4 B.-6 C.-8 D.-10
3．△ABC的三边a、b、c成等比数列，确定公比的取值范围是 ( )
A．(0，
) B.(
，+∞)
C.(，) D.［1，］
4．已知a1,a2,a3,a4,a5,a6,a7,a8为各项都大于零的数列，命题①a1,a2,a3,a4,a5,a6,a7,a8不是等比数列；命题②a1+a8<a4+a5,则命题②是命题①的 ( )
A.充分且必要条件 B.即不充分也不必要条件
C.必要但不充分条件 D.充分但不必要条件
5．等差数列{an}中,公差d<0,n≥2时,前n项和为Sn,则有 ( )
A.Sn≥na1 B.Sn≤nan C.nan<Sn<na1 D.na1<Sn<nan
6．一个小球从100m高处自由落下，每次着地后又跳回到原高度的一半再落下，设它第n次着地时，共经过了anm，n≥2，则有 ( )
A.an＝an-1+
B.an＝an-1+
C.an＝an-1+
D.an＝
an-1+
7．在等差数列{an}中,an≠0,an+1-a
+an-1=0(n≥2),若S2n-1=38,则n的值是 ( )
A.38 B.10 C.20 D.9
二、填空题(4×3′＝12′)
8．若x≠y，两个数列x，a1，a2，y和x，b1，b2，b3，y分别成等差数列，那么
＝ .
9．已知等差数列｛an｝，｛bn｝的前n项和分别为Sn与Tn，若
.
10．设Sn为数列{an}的前n项和，“若Sn=an2+bn+c,则{an}为等差数列”是真命题，记该命题的逆命题为P，否命题为Q，逆否命题为R，则P、Q、R中是真命题的有 个.
11．数列{an}的前n项和Sn=n2+n,则a5+a6+a7+a8 .(n∈N)
三、解答题(5×10′＝50′)
12．设函数f(x)=log2x-logx2(0<x<1),数列{an}满足f(2an)=2n(n∈N).
(1)求数列{an}的通项公式;
(2)判定数列的单调性.
13．在
和n+1之间插入n个正数，使这n+2个数依次成等比数列，求所插入的n个数之积.
14．已知一个项数为偶数，首项为1的等比数列，其奇数项的和为85，偶数项的和为170，求这个等比数列的公比q及项数n.
15．数列{an}的前n项和记为Sn,已知a1=1,an+1=
Sn(n=1,2,3,…).证明：
(1)数列{
}是等比数列;
(2)Sn+1=4an.
16．某工厂年度初借款A元，从该年度末开始，每年偿还一定金额x元，恰在n年内还清(包括借款的利息)，借款的年利率为r，求每年偿还的金额.
四、思考与讨论(10′)
17．对任意函数f(x),x∈D，可按图所示构造一个数列发生器，其工作原理如下：
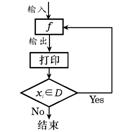①输入数据x0∈D，经数列发生器输出x1=f(x0)；
②若x1
D，则数列发生器结束工作；若x1∈D，则将x1反馈回输入端，
再输出x2=f(x1)，并依此规律继续下去．现定义f(x)=
.
(1)若输入x0=
，则由数列发生器产生数列{xn}，请写出数列{xn}
的所有项(n∈N)；
| |
x0的值；
(3)若输入x0时，产生的无穷数列{xn}满足：对任意正整数n，均有xn<xn+1，求x0的取值范围．
参考答案
1．B an=0时，A、D均可排除，当a1<0，q>1时｛an｝递减，排除C.
2．B ∵a1,a3,a4成等比数列,∴a
=a1·a4,∴(a2+2)2=(a2-2)(a2+4),∴a2=-6.
3．C 设三边为a，aq,aq2，若0<q<1，则aq+aq2>a.
∴<q<1，若q>1，则a+aq>aq2，此时1<q<，若q=1，符合，
∴q∈（，）.
4．D 假设数列为等比数列,公比为q,则(a1+a8)-(a4+a5)=a1(1-q3)(1-q4)≥0,故②
①；
假设数列为等差数列，则a1+a8=a4+a5,故①
②,选D.
5．C ∵d<0,∴a1>a2>a3>…>an,∴na1>Sn>nan.
6．B an＝100+50×2+25×2＋…+100×()n-1×2(n≥2)
＝100+2×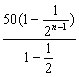
＝300-200×
，
∴an-an-1＝200(
-)＝
，即an＝an-1＋.
7．B ∵{an}为等差数列,∴an+1-a+an-1=2an-a=0.又an≠0,∴an=2.
故等差数列每项均为2,则S2n-1=38=19×2.即2n-1=19,n=10.故选B.
8．
d1＝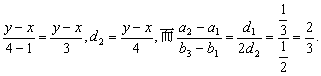
9．
.
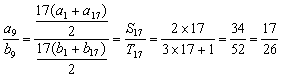10．3 逆命题“若{an}为等差数列，则Sn=an2+bn+c”为真命题，由四种命题原命题与逆否命题等价，逆命题与否命题等价，有P、Q、R都为真命题.
11．52 a5+a6+a7+a8=S8-S4=72-20=52．
12．解 (1)由已知得,f(x)=log2x-
,
∴f(2an)=log22an-
=log22an-
2=an-
=2n,
a-2nan-1=0,解之得an=n±
,因为0<x<1,
所以0<2an<1,an<0,故an=n-(n∈N*);
(2)因为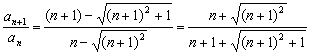
<1,
而an<0(n∈N),所以an+1>an,故{an}是单调递增数列.
点评 运用函数与数列的关系解题，是高考中常考的一个知识点，要认真体会.
13．解 n+1＝qn+1qn+1＝n(n+1).
设n个数之积为p,则p＝()nq·q2·q3·…·qn，
∴p＝()nq1＋2＋…+n＝()n·
.
14．解 a2+a4+…+a2n＝170 ①
a1+a3+…+a2n-1＝85 ②
①÷②得q＝2，Sn＝
＝255，∴2n＝256，n=8.
15．分析 （1）将已知递推关系式中an+1用Sn＋1－Sn表示，将其化为只含有和的关系式求解.
(2)由（1）和已知结合，通过构造法即可得证.
证明 （1）∵an+1=Sn+1-Sn,an+1=Sn,∴(n+2)Sn=n(Sn+1-Sn),整理得:nSn+1=2(n+1)Sn,
所以
是以2为公比的等比数列.
(2)由(1)知
=4·
(n≥2).
于是Sn+1=4(n+1)·=4an(n≥2).
又a2=3S1=3,故S2=a1+a2=4.
因此对于任意正整数n≥1,都有Sn+1=4an.
点评 本题求证结论含有Sn,一般先用an+1=Sn+1-Sn公式把题中所给的关系式化为Sn的递推关系，这是本题一个灵活之处，考查了同学们的灵活运用所学知识的能力，而第二问又考查了分析问题的推理能力.
16．解 第一年年末欠款为A(1+r)-x，第二年年末欠款为［A(1+r)-x］(1+r)-x＝A(1+r)2-x［(1+r)+1］，…第n年年末欠款A(1+r)n-x［（1＋r）n-1+(1+r)n-2+…+(1+r)+1］，
由题意得A(1+r)n-x［(1+r)n-1+(1+r)n-2+…+(1+r)+1］＝0，
∴A(1+r)n=x·
，∴x=
.
17．解 (1)∵f(x)的定义域D=(-∞,-1)∪(-1,+∞)．
当x0=时，x1=f(x0)=f()=
∈D．
同理求得x2=f(x1)=
∈D，x3=f(x2)=-1D．
∴数列{xn}只有三项:，，-1.
(2)由f(x)=x，即=x,∴x2-3x+2=0，得x=1或x=2.
∴当x0=1或x0=2时，xn+1=
=xn．
因此，当x0=1时，xn=1；当x0=2时，xn=2,n∈N．
(3)解不等式x<,得x<-1或1<x<2.
∵对任意正整数n均有xn<xn+1，∴要使x1<x2，则x1<-1或1<x1<2．
对于函数f(x)==4-
,若x1<-1，则x2=f(x1)>4;x3=f(x2)<4<x2，应排除．
若1<x1<2，则x2=f(x1)>x1，且1<x2<2．
依此类推，可得数列{xn}的所有项均满足xn+1>xn，
由1<x1<2，即1<
<2得x0∈(1,2)即为所求x0的取值范围．