专题考案(1)函数板块 第5课 函数的应用

(时间：90分钟　满分：100分)

题型示例

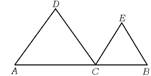已知线段AB=2l，在其上作一点C，欲使以AC，BC为边的两正三角

形面积的和最小，问C点应取在何处？

分析1　设AC=x,两个正三角形的面积可化为x的二次函数.

图1

解　设两个正三角形面积分别为S₁和S₂，如图1所示，设AC=x,

S₁=x²,S₂=(2l-x)²,

∴S=S₁+S₂=［(2l-x)²+x²］=x²-lx+l²,用二次函数顶点坐标公式求得：当x===l时，S_min==l².

所以当C点在AB中点时，S最小.

分析2　由上面得S=x²-lx+l²,用配方法求出S的最小值.

解　由S=x²-lx+l²,配方可得S=(x-l)²+l²,显然当x=l时，S取得最小值,S_min=l².故当C点在AB中点时，S取得最小值.

点评　本题通过二次函数建立模型，来找到两个三角形面积和的关系.从以上解析可以看出，本问题实质是已知三角形的边求其面积问题，其关键在于找出边与面积的函数关系，这也是解决有关面积问题的最重要的一环.

一、选择题(8×4′＝32′)

1．某种细胞分裂时，由1个分裂成2个，2个分裂成4个，…，一个这样的细胞分裂x次后，得到的细胞个数y与x的函数关系式是　　　　　　　　　　　　　　　　 (　　)

A.y=2x(x∈N*)　　　　　　  B.y=2x(x∈N*)

C.y=2x+1(x∈N*)　　　　　  D.y=log₂x(x∈N*)

2．一种产品的成本原来为a元，计划在今后m年内使成本平均每年比上一年降低P%，则成本y与经过的年数x的函数关系式为　　　　　　　　　　　　　　　　　　 (　　)

A.y=a(1-P%)^x　　 B.y=a(P%)^x　　 C.y=a-(P%)^x　　 D.y=a(1＋P%)^x

3．某工厂第三年的产量比第一年的产量增长44%，若每年的平均增长率相同(设为x)，则以下结论正确的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　)

A.x>22%　　 B.x<22%　　 C.x=22%　　 D.x的大小由第一年的产量确定

4．拟定从甲地到乙地通话m  min的电话费由f(m)=1.06(0.5×［m］+1)给出，其中m>0,［m］是大于或等于m的最小整数(如［3］=3,［3.7］=4,［3.1］=4),则从甲地到乙地通话时间为5.5min的话费为　　　　　　　　　　　　　　　　　　　　　　　　　　　  (　　)

A.3.71　　　　 B.3.97　　　　  C.4.24　　　　  D.4.77

5．将进货单价为80元的商品按90元一个售出时，能卖出400个，已知该商品每个涨价1元，其销售量就减少20个，为了赚得最大利润，售价应定为　　　　　　　　 (　　)

A.每个110元　　B.每个105元　　C.每个100元　　D.每个95元

6．对广东省某县农村抽样调查，结果如下：电冰箱拥有率49%，电视机拥有率85%，洗衣机拥有率44%，至少拥有上述三种家用电器中两种以上的占63%，三种电器齐全的占25%，那么一种电器也没有的相对贫困户所占比例为　　　　　　　　　　　　　　　 (　 )

A.35%　　　 B.10%　　　 C.15%　　　 D.资料不全，难以判断

7．某商店出售A、B两种价格不同的商品，由于商品A连续两次提价20%，同时商品B连续两次降价20%，结果都以每件23元售出，若商店同时售出这两种商品各一件，则与价格不升不降时情况比较，商店赢利情况是　　　　　　　　　　　　　　　　　 (　　)

A.多赚约6元　　B.少赚约6元　　C.多赚约2元　　D.赢利相同

8．对于函数f(x)和g(x)，其定义域均为［a,b］，若对任意的x∈［a,b］，总有，则称f(x)可被g(x)置换，那么下列给出的函数中能置换f(x)=(4≤x≤16)的是　 (　　)

A.g(x)=(x+6)(4≤x≤16)　　　　B.g(x)=x²+6(4≤x≤16)

C.g(x)=x+6(4≤x≤16)　　　　　  D.g(x)=2x+6(4≤x≤16)

二、填空题(4×4′＝16′)

9．已知A、B两地相距150ｋｍ，某人开汽车以60ｋｍ／ｈ的速度从A地到达B地，在B地停留1h后再以50ｋｍ／ｈ的速度返回A地，把汽车离开A地的距离x表示为时间t的函数，表达式是　　　　　 .

10．现有含盐7%的食盐水200ｇ，要将它制成工业生产上需要的含盐在5%以上且在6%以下(不含5%和6%)的食盐水，设需要加入4%的食盐水xｇ，则x的取值范围是　　　　  .

11．某卡车在同一时间段里速度v(km/h)与耗油量θ(kg/h)之间有近似的函数关系式:θ=0.0025v²-0.175v+4.27,则车速为　　　　km/h时,卡车的耗油量最少.

12．若关于x的方程2^2x+2^xa+a+1=0有实根，则实数a的取值范围是　　　　.

三、解答题(4×10′＋12′＝52′)

13．运货卡车以xkm/h的速度匀速行驶130km，按交通法规限制速度为50≤x≤100(单位：km/h).假设汽油的价格是每升2元，而汽车每小时耗油(2+)L，司机的工资是每小时14元.

(1)求这次行车总费用y关于x的表达式；

(2)当x为何值时，这次行车的总费用最低，并求出最低费用的值.(取≈3.16)

14．现有直径为d的圆木，要把它锯成横截面为矩形的梁，从材料力学知道，横截面为矩形的木梁的强度Q与梁宽和梁高的平方的乘积成正比.问如何截法才能使梁的强度最大?

15．政府收购某种农产品的原价格是200元/担，其中征税标准为每100元征10元(叫税率为10个百分点，即10%)，计划可收购a万担，为了减轻农民负担，现决定将税率降

低x个百分点，预计收购量可增加2x个百分点.

(1)写出税收y(万元)与x的函数关系式.

(2)要使此项税收在税率调节后不低于原计划税收的83.2%，试确定x的范围.

16．我国是一个水资源比较贫乏的国家，各地常采用价格调控等手段来达到节约用水的目的.已知某市的用水收费公式是：水费=基本费+超额费+损耗费.若每月用水量不超过最低限量am³,只付基本费8元和每户每月的固定损耗费c元；若用水量超过am³时，除了付同上的基本费和损耗费外，超过部分每立方米付b元的超额费，已知损耗费c不超过5元.该市某家庭今年1~6月份的用水量和1~3月份的水费如下表：

月份	一月	二月	三月	四月	五月	六月
用水量/m3	9	15	22	25	8	31
水费/元	9	19	33

请根据上面表格的数据，分别计算该家庭4~6月份的水费.

17．设P=，函数y=log₂(ax²-2x+2)的定义域为Q．

(1)若方程log₂(ax²-2x+2)=2在P内有解，求实数a的范围；

(2)若P∩Q≠，求实数a的范围．

参考答案

1．B　从第二年开始，每年的细胞数是前一年的2倍.

2．A　成本每年比上一年降低P%，即每年是上一年的(1-P%)倍.

3．B　设第一年的产量为A，则第三年的产量为A(1+x)²，依题意A(1+x)²=A(1+44%)，即(1+x)²=1+44%>1+2xx<22%.

4．C　f(5.5)=1.06(0.5×［5.5］+1)=4.24.

5．D　设该商品每个涨价a元，则利润y=(90+a-80)(400-20a)(a=0,1，2,…)，即

y=20(a+10)(20-a)=-20(a-5)²+4500，∴a=5即定价为95元时，y有最大值.

6．B　至少有一种家用电器的用户占［49+85+44-(63+25)］%=90%,故一种家用电器也没有的用户占10%.

7．B　设A、B两种商品的原价为a、b，则a(1+20%)²=b(1-20%)²=23a=,

b=，a+b-46≈6元.

8．A　4≤x≤16，．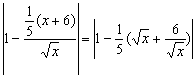

由y=t+的单调性知2≤+≤5，(+)≤

∴≤.

(0<x≤2.5) (2.5≤t≤3.5) (3.5<t≤6.5)

9．x=　

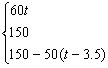
10．100<x<400  5%<<6%，解得100<x<400.

11．35　将已知函数配方得θ=0.0025(v-35)²+1.2075,∴v=35时θ最小.

12．(-∞，2-2)　设t=2^x,则t²+at+a+1=0有正根．

由Δ=a²-4(a+1)≥0a≥2+2或a≤2-2.

a≥2+2时，t₁+t₂=-a<0，t₁t₂=a+1>0无正根．

a≤2-2时，t₁+t₂=-a>0，必有正根．

13．解　(1)设所用时间为t=(h),y=×2×(2+)+,x∈［50,100］.

所以，这次行车总费用y关于x的表达式是y=x,x∈［50,100］,

即y=x,x∈［50,100］.

(2)y=x≥26≈82.16(元),

当且仅当x,即x=18≈56.88时，上述不等式中等号成立.

答:当x约为56.88km/h时，这次行车的总费用最低，最低费用约为82.16元.

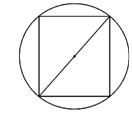14．解　引入自变量建立目标函数，设梁宽为x,则高为,(如图3所示)

∴Q=kx(d²-x²)=kkd³

图3

当2x²=d²-x²,即x=d时,取得最大强度.此时高=d.

点评　引入自变量，建立目标函数，是解决最值问题的重要方法，此法的关键

是引入适当的自变量，对变量有两点要求:①容易建立目标函数;②函数最值易求.

15．解　(1)调节后的税率为(10-x)%，预计可收购a(1+2x%)万担，总金额200a(1+2x%)万元.

依题意y=200a(100+2x)(10-x)×10^-4=a(100+2x)(10-x)　(0<x<10).

(2)原计划税收为200a×10%=20a万元，依题意有a(100+2x)(10-x)≥20a×83.2%，整理得x²+40x-84≤0-42≤x≤2，又x>0，∴0<x≤2.

16．解　设每月用水量为xm³时，水费为y元，依题意

y=因0<c≤5,所以8<8+c≤13,由表格数据知，第二、三月份的水费均大于13元，故用水量都大于最低限量am³,从而有

如果一月份的用水量也超过最低限量，则8+2(9-a)+c=9,即2a=c+17这与（*）矛盾，故一月份的用水量未超过最低限量.

故c+8=9c=1,由此得a=10,b=2,c=1.

从而可计算4~6月份的水费分别为39元，9元，51元.

17．解　(1)由log₂(ax²-2x+2)=2得ax₂-2x+2=4.

ax²-2x-2=0在［，2］内有解．

∴a=2(+)²-,∵≤≤2，∴≤a≤12.

(2)∵P∩Q≠，∴在［，2］上至少有一个值使ax²-2x+2>0成立．

∵≤x≤2，∴a>，又-4≤≤.∴a>-4即为所求．