高考理科数学级第二次模拟考试
理科数学试卷
一、选择题:(本大题共8个小题,每小题5分,共40分)
1.设集合![]() ,
,![]() ,若U=R,且
,若U=R,且![]()
![]() ,则实数m的取值范围是( )
,则实数m的取值范围是( )
A.m<2 B.m≥2 C.m≤2 D.m≤2或m≤-4
2.不等式![]() 成立的充分不必要条件是
成立的充分不必要条件是
A.![]() 或
或![]() B.
B.![]() C.
C.![]() 或
或![]() D.
D. ![]()
3.![]() = ( )
= ( )
(A)tana (B)tan2a
(C)1 (D)![]()
4.圆![]() 上与直线
上与直线![]() 的距离等于
的距离等于![]() 的点共有
的点共有
A.1个 B.2个 C.3 个 D.4个
5..设两个非零向量![]() 不共线,若
不共线,若![]() 与
与![]() 也不共线,则实数k的取值范围为
也不共线,则实数k的取值范围为
( ).
A.![]() B.
B.![]()
C.![]() D.
D. ![]()
6. 三棱锥D—ABC的三个侧面分别与底面全等,且AB=AC=![]() ,BC=2,则二面角A—BC—D的大小为
,BC=2,则二面角A—BC—D的大小为
A. 300 B. 450 C.600 D.900
7. 等比数列![]() 前
前![]() 项的积为
项的积为![]() ,若
,若![]() 是一个确定的常数,那么数列
是一个确定的常数,那么数列![]() ,
,![]() ,
,![]() ,
,![]() 中也是常数的项是( )
中也是常数的项是( )
A. ![]() B.
B. ![]() C .
C .![]() D.
D. ![]()
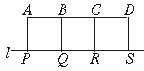 8.如右图,A、B、C、D是某煤矿的四个采煤点,l是公路,图中所标线段为道路,ABQP、BCRQ、CDSR近似于正方形.已知A、B、C、D四个采煤点每天的采煤量之比约为5∶1∶2∶3,运煤的费用与运煤的路程、所运煤的重量都成正比.现要从P、Q、R、S中选出一处设立一个运煤中转站,使四个采煤点的煤运到中转站的费用最少,则地点应选在(
)
8.如右图,A、B、C、D是某煤矿的四个采煤点,l是公路,图中所标线段为道路,ABQP、BCRQ、CDSR近似于正方形.已知A、B、C、D四个采煤点每天的采煤量之比约为5∶1∶2∶3,运煤的费用与运煤的路程、所运煤的重量都成正比.现要从P、Q、R、S中选出一处设立一个运煤中转站,使四个采煤点的煤运到中转站的费用最少,则地点应选在(
)
A. S点 B.Q点 C.R点 D. P点
二. 填空题(本大题共6个小题,每小题5分,共30分)
9.若![]() 的内角
的内角![]() 满足
满足![]() ,则
,则![]() _______
_______
10.已知函数![]()
11.一个正四棱锥的底面边长为2,侧棱长为![]() ,五个顶点都在同一个球面上,则此
,五个顶点都在同一个球面上,则此
球的表面积为
12. 若函数![]() 的递减区间为(
的递减区间为(![]() ,
,![]() ),则a的取值范围是
),则a的取值范围是
13.实数![]() 满足
满足![]() ,则
,则![]() 的最大值是
的最大值是
14.设函数![]() ,给出以下四个论断:
,给出以下四个论断:
①![]() 的周期为π; ②
的周期为π; ②![]() 在区间(-
在区间(-![]() ,0)上是增函数;
,0)上是增函数;
③![]() 的图象关于点(
的图象关于点(![]() ,0)对称; ④
,0)对称; ④![]() 的图象关于直线
的图象关于直线![]() 对称.
对称.
以其中两个论断作为条件,另两个论断作为结论,写出你认为正确的一个命题:
![]() (只需将命题的序号填在横线上).
(只需将命题的序号填在横线上).
 答题卷
答题卷
一、选择题答题卡(共8个小题,每小题5分,共40分)。
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 答案 |
|
|
|
|
|
|
|
|
二、填空题(共6个小题,每小题5分,共30分).
9、 10、 11、
12、 13、 14、
三、解答题:(本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.)
15、(本小题满分12分)
已知集合![]() 函数
函数![]()
(1)求![]() 的最大值及最小值;
的最大值及最小值;
(2)若不等式![]() 上恒成立,求实数。的取值范围.
上恒成立,求实数。的取值范围.
16. (本小题满分13分)已知向量![]() 满足
满足![]() ,且
,且![]() ,令
,令![]() ,
,
(Ⅰ)求![]() (用
(用![]() 表示);
表示);
(Ⅱ)当![]() 时,f(x)
时,f(x)![]() x2-2tx-
x2-2tx-![]() 对任意的
对任意的![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围。
的取值范围。
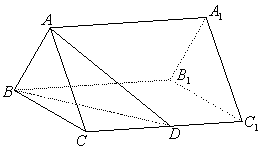 17. (本小题满分14分) 如图,已知正三棱柱
17. (本小题满分14分) 如图,已知正三棱柱![]() —
—![]() 的底面边长是
的底面边长是![]() ,
,![]() 是侧棱
是侧棱![]() 的中点,直线
的中点,直线![]() 与侧面
与侧面![]() 所成的角为
所成的角为![]() .
.
(Ⅰ)求此正三棱柱的侧棱长;
(Ⅱ) 求二面角![]() 的平面角的余弦值大小;
的平面角的余弦值大小;
(Ⅲ)求点![]() 到平面
到平面![]() 的距离.
的距离.
18. (本小题满分14分)(本小题14分)设![]()
![]() ,令
,令![]() ,
,![]() ,
,
又![]() ,
,![]() .
.
(1)判断数列![]() 是等差数列还是等比数列并证明; (2)求数列
是等差数列还是等比数列并证明; (2)求数列![]() 的通项公式;
的通项公式;
(3)求数列![]() 的前
的前![]() 项和.
项和.
19、设O为坐标原点,曲线![]() 上有两点P、Q满足关于直线
上有两点P、Q满足关于直线![]() 对称,又以PQ为直径的圆过O点.
对称,又以PQ为直径的圆过O点.
(1)求![]() 的值;
(2)求直线PQ的方程.
的值;
(2)求直线PQ的方程.
20.(本小题满分14分)已知函数![]() 和
和![]() 的图象在
的图象在![]() 处的切线互相平行.
处的切线互相平行.
(Ⅰ) 求![]() 的值;
的值;
(Ⅱ)设![]() ,当
,当![]() 时,
时,![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
参考答案
一、选择题答题卡(共8个小题,每小题5分,共40分)。
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 答案 | B | D | B | C | A | D | C | B |
二、填空题(本大题共6个小题,每小题5分,共30分).
9.![]() 10.
10. ![]() 11. 9π 12. a>0
11. 9π 12. a>0
13. 7 14 ①④![]() ②③ 或 ①③
②③ 或 ①③![]() ②④
②④
三、解答题:(本大题共2小题,共30分.解答应写出文字说明,证明过程或演算步骤.)
15.解:解:(1)∵![]()
![]()
又∵![]()
即![]()
![]()
(2)∵![]()
![]()
![]()
16.【解析】(Ⅰ)由题设得![]() ,对
,对![]() 两边平方得
两边平方得
![]() …………………………………………………………2分
…………………………………………………………2分
展开整理易得![]() ……………………………………………………5分
……………………………………………………5分
(Ⅱ)![]() ,当且仅当
,当且仅当![]() =1时取得等号. ……………………………7分
=1时取得等号. ……………………………7分
欲使![]() 对任意的
对任意的![]() 恒成立,等价于
恒成立,等价于![]() ……………9分
……………9分
即![]() 在
在![]() 上恒成立,而
上恒成立,而![]() 在
在![]() 上为单调函数或常函数,
上为单调函数或常函数,
所以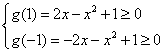 ………………………………………………………………11分
………………………………………………………………11分
解得![]() …………………………………………………………………………13分
…………………………………………………………………………13分
故实数![]() 的取值范围为
的取值范围为![]() ………………………………………………………14分
………………………………………………………14分
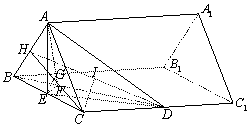 17. 解:(Ⅰ)设正三棱柱
17. 解:(Ⅰ)设正三棱柱![]() —
—![]() 的侧棱长为
的侧棱长为![]() .取
.取![]() 中点
中点![]() ,连
,连![]() .
.
![]() 是正三角形,
是正三角形,![]() .
.
又底面![]() 侧面
侧面![]() ,且交线为
,且交线为![]() .
.
![]() 侧面
侧面![]() .
.
连![]() ,则直线
,则直线![]() 与侧面
与侧面![]() 所成的角为
所成的角为![]() . ……………2分
. ……………2分
在![]() 中,
中,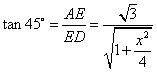 ,解得
,解得![]() . …………3分
. …………3分
![]() 此正三棱柱的侧棱长为
此正三棱柱的侧棱长为![]() .
……………………4分
.
……………………4分
注:也可用向量法求侧棱长.
(Ⅱ)解法1:过![]() 作
作![]() 于
于![]() ,连
,连![]() ,
,
![]() 侧面
侧面![]()
![]()
![]() .
.
![]() 为二面角
为二面角![]() 的平面角.
……………………………6分
的平面角.
……………………………6分
在![]() 中,
中,![]() ,又
,又
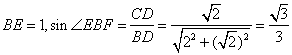 ,
, ![]()
![]() .
.
又![]()
![]() 在
在![]() 中,
中,![]() .
…………………………8分
.
…………………………8分
故二面角![]() 的大小为
的大小为![]() .
…………………………9分
.
…………………………9分
解法2:(向量法,见后)
(Ⅲ)解法1:由(Ⅱ)可知,![]() 平面
平面![]() ,
,![]() 平面
平面![]() 平面
平面![]() ,且交线为
,且交线为![]() ,
,![]() 过
过![]() 作
作![]() 于
于![]() ,则
,则![]() 平面
平面![]() .
…………10分
.
…………10分
在![]() 中,
中,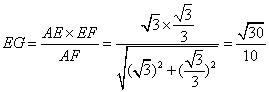 .
…………12分
.
…………12分
![]()
![]() 为
为![]() 中点,
中点,![]() 点
点![]() 到平面
到平面![]() 的距离为
的距离为![]() . …………13分
. …………13分
解法2:(思路)取![]() 中点
中点![]() ,连
,连![]() 和
和![]() ,由
,由![]()
![]() ,易得平面
,易得平面![]() 平面
平面![]() ,且交线为
,且交线为![]() .过点
.过点![]() 作
作![]() 于
于![]() ,则
,则![]() 的长为点
的长为点![]() 到平面
到平面![]() 的距离.
的距离.
解法3:(思路)等体积变换:由![]() 可求.
可求.
解法4:(向量法,见后)
题(Ⅱ)、(Ⅲ)的向量解法:
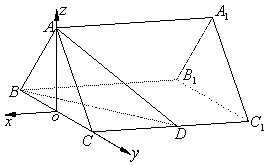 (Ⅱ)解法2:如图,建立空间直角坐标系
(Ⅱ)解法2:如图,建立空间直角坐标系![]() .
.
则![]() .
.
设![]()
![]() 为平面
为平面![]() 的法向量.
的法向量.
由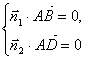 得
得![]()
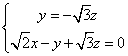 .
.
![]() 取
取![]() …………6分
…………6分
又平面![]() 的一个法向量
的一个法向量![]() …………7分
…………7分
![]()
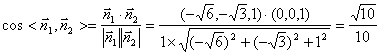 . …………8分
. …………8分
结合图形可知,二面角![]() 的大小为
的大小为![]() .
…………9分
.
…………9分
(Ⅲ)解法4:由(Ⅱ)解法2,![]()
![]() …………10分
…………10分
![]() 点
点![]() 到平面
到平面![]() 的距离
的距离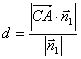
 =
=![]() .13分
.13分
18. 解:(1) 由![]() 得:
得: ![]() ,……(2分)
,……(2分)
变形得: ![]() 即:
即:![]() , ………(4分)
, ………(4分)
![]() 数列
数列![]() 是首项为1,公差为
是首项为1,公差为![]() 的等差数列. ………(5分)
的等差数列. ………(5分)
(2) 由(1)得:![]() , ………(7分)
, ………(7分)
![]() ,
, ![]()
![]() ………(9分)
………(9分)
(2)
由(1)知: ![]() ………(11分)
………(11分)
![]()
![]()
![]() ………(14分).
………(14分).
19、20.解: (1) 曲线![]() 表示以
表示以![]() 为圆心,以3为半径的圆, 圆上两点P、Q满足关于直线
为圆心,以3为半径的圆, 圆上两点P、Q满足关于直线![]() 对称,则圆心
对称,则圆心![]() 在直线
在直线![]() 上,代入解得
上,代入解得 ![]() -------------------------------------3分
-------------------------------------3分
(2)直线PQ与直线![]() 垂直,所以设PQ方程为
垂直,所以设PQ方程为
![]() ,
,![]()
![]() .
.
将直线![]() 与圆的方程联立得
与圆的方程联立得![]()
由![]() 解得
解得![]() .----------------------5分
.----------------------5分
![]() .
.
又以PQ为直径的圆过O点
![]()
![]() 解得
解得![]()
![]() -----------------10分
-----------------10分
故所求直线方程为![]() -----------------------------------------------------------12分
-----------------------------------------------------------12分
20.解:(Ⅰ) ![]() ………………………3分
………………………3分
∵函数![]() 和
和![]() 的图象在
的图象在![]() 处的切线互相平行
处的切线互相平行
![]() …………………………………………………5分
…………………………………………………5分
![]()
![]() ………………………………………………………………6分
………………………………………………………………6分
(Ⅱ)![]()
![]()
![]()
![]() …………………………………………7分
…………………………………………7分
令![]()
![]()
∴当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() .
.
∴![]() 在
在![]() 是单调减函数,在
是单调减函数,在![]() 是单调增函数. …………………………9分
是单调增函数. …………………………9分
![]() ,
,![]()
∴当![]() 时,有
时,有![]() ,当
,当![]() 时,有
时,有![]() .
.
∵当![]() 时,
时,![]() 恒成立, ∴
恒成立, ∴![]() …………………………11分
…………………………11分
∴满足条件的![]() 的值满足下列不等式组
的值满足下列不等式组
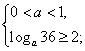 ①,或
①,或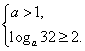 ②
②
不等式组①的解集为空集,解不等式组②得![]()
综上所述,满足条件的![]() 的取值范围是:
的取值范围是:![]() . ……………………13分
. ……………………13分
