专题考案(3)三角板块 第2课 三角函数的图象

 (时间：90分钟　满分：100分)

题型示例

已知向量a=(cosx,2sinx),b=(2cosx,cosx),f(x)=a·b+m(m为常数).

(1)求f(x)的最小正周期；

(2)若f(x)在上的最大值与最小值之和为3，求m的值;

(3)在(2)的条件下,f(x)按向量(h,k)平移后得到y=2sin²x的图象，其中h<,求h,k的值.

解　∵a=(cosx,2sinx),b=(2cosx,cosx),

∴a·b=cosx·2cosx+2sinx·cosx=2cos²x+sin²x=1+cos²x+sin²x=2sin(2x+)+1.∴f(x)=a·b+m=2sin(2x+)+m+1.

(1)f(x)的最小正周期T=π.

(2)∵f(x)在上是单调递增函数，∴f(x)在上的最大值为f()，最小值为f(-),而由题意f(x)在上的最大值与最小值之和为3,可得f()+f(-)=3，解得m=0,

(3)当m=0时，f(x)=2sin(2x+)+1.

设P(x,y)为f(x)的图象上的任意一点，此点按向量(h,k)平移后与Q(x′,y′)相对应，则由

平移公式得，代入y=2sin²x得y+k=2sin［2(x+h)］，与f(x)=2sin(2x+)+1应是同一个函数，比较系数可得h=,k=-1.

点评　本题主要考查了三角函数的周期的求法和图象的平移等知识，但已知条件用向量的数量积进行了“伪装”，使得题目的隐蔽性变得更强，难度更大.在求解时仍要先化简f(x)的解析式，利用周期的计算公式求出函数的周期，利用平移公式求平移前的函数解析式，最后比较系数求得h和k的具体值.

一、选择题(8×3′＝24′)

1．为了得到函数y=sin(2x-)的图象，可以将函数y=cos²x的图象　　　　　　　 (　  )

A.向右平移个单位长度　　 B.向右平移个单位长度

C.向左平移个单位长度　　 D.向左平移个单位长度

图1

2．与图1中曲线对应的函数是　　　　　　　 (　　)

A.y=sinx　　 B.y=sinx　　 C.y=-sinx　　 D.y=-sinx

3．已知函数y=Asin(ωx+φ)+m的最大值为4，最小值为0，最小正周期为，直线x=是其图象的一条对称轴，则下列各式中符合条件的解析式是　　　　　　　　　　 (　　)

A.y=4sin(4x+)　　　　 B.y=2sin(2x+)+2

C.y=2sin(4x+) 　　　　D.y=2sin(4x+)+2

4．若f(x)=tan,则　　　　　　　　　　　　　　　　　　　　　　　　　 (　　)

A.f(0)>f(-1)>f(1)　　　 B.f(0)>f(1)>f(-1)

C.f(1)>f(0)>f(-1)　　　 D.f(-1)>f(0)>f(1)

5．已知函数y₁=3sin(2x-)，y₂=4sin(2x+)，那么函数y=y₁+y₂的振幅A的值是　(　　)

A.5　　　　  B.7　　　　  C.13　　　　  D.

6．下列函数中同时满足①在区间(0,)上是增函数，②以π为周期，③是偶函数三个条件的是　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　 (　　)

A.y=tanx　　 B.y=e^-cosx 　　C.y=sinx　　 D.y=sinx

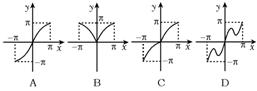
7．函数y=x+sinx，x∈［-π，π］的大致图象是图2中的　　　　　　　　 (　　)

		图2

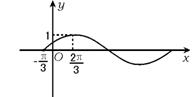
8．若函数f(x)=sin(ωx+φ)的图象(部分)如图3所示，则ω和φ的取值是　　 (　　)

A.ω=1,φ=　　　　

B.ω=1,φ=-

图3

C.ω=,φ=　　　

D.ω=,φ=-

二、填空题(5×4′＝20′)

9．将函数y=f(x)sinx(x∈R)的图象向右平移个单位后，再作关于x轴的对称变换，得到函数y=1-2sin²x的图象，则f(x)可以是　　　　 .

10．函数y=2sin(kx-)的周期为T,且T∈(1,3),则正整数k的最大值是　　　　  .

11．由函数y=2sin3x()与函数y=2(x∈R)的图象围成一个封闭图形，这个封闭图形

的面积是　　　　  .

12．设函数f(x)=sin(ωx+φ)(ω>0,),给出以下四个论断：

①它的图象关于直线x=对称；②它的周期为π；

③它的图象关于点(,0)对称；④在区间［-,0］上是增函数.

以其中两个论断作为条件，余下论断作为结论，写出你认为正确的两个命题：

(1)　　　　　　  ；(2)　　　　　　  .

13．函数y=Asin(ωx+θ)(其中A>0,ω>0,θ<)的图象的一条对称轴的方程是x=，一个最高点的纵坐标是3，要使该函数的解析式为y=3sin(2x+)，还应给出一个条件是　　　　　  .

三、解答题(3×12′＝36′)

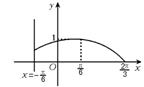14．已知定义在区间［-π,π］上的函数y=f(x)的图象关于直线x=-对称，当x∈［-，π］时，函数f(x)=Asin(ωx+φ)(A>0,ω>0,-<φ<)的图

象如图4所示.

(1)求函数y=f(x)在［-π, π］上的表达式；

图4

(2)求方程f(x)=的解.

15．设0<θ<2π,且方程2sin(θ+)=m有两个不同的实数根，求实数m的取值范围及这两个实根的和.

16．已知函数f(x)=2cosx·sin(x+)-sin²x+sinx·cosx.

(1)求函数f(x)的最小正周期;

(2)求f(x)的最小值及取得最小值时相应的x值;

(3)若当x∈时,f(x)的反函数为f ^-1(x),求f ^-1(1)的值.

四、思考与讨论(20′)

17．已知=cosπt-sinπt,=cos²πt-sin²πt,其中-1≤t≤1.

(1)作出函数x=f(t)的图象；

(2)写出函数y=g(x)的解析式，并作出函数y=g(x)的图象．

参考答案

1．B　y=sin(2x-)=cos［-(2x-)］=cos(-2x+π)=cos(2x-π)

=cos2(x-)，故可以将函数y=cos2x的图象向右平移个单位长度得

到y=sin(2x-)的图象.

2．C　由图象知函数为偶函数，又x>0时，y=-sinx;x<0时，y=sinx，

∴所求函数为y=-sinx.

3．D　A=2,m=2.ω>0时，,ω=4.y=2sin(4x+φ)+2.

令4x+φ=kπ+,k∈Z,且x=，则π+φ=kπ+,得φ=kπ-π,

φ的一个值为.

4．A　作出函数f(x)=tan(x+)的图象如图5所示，易知:f(0)>f(-1)>f(1).

图5

5．D　y=y₁+y₂=3sin(2x-)+4sin(2x+)=sin2x-cos2x+2sin2x+2cos2x

=sin2x+cos2x= 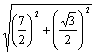sin(2x+φ)=sin(2x+φ).

(其中cosφ=,sinφ=)

6．D　y=tanx不是偶函数，从而否定A;y=e^-cosx以2π为周期函数，从而否定B;

y=sinx不是周期函数，从而否定C;y=sinx在(0,)上是增函数，以π为周期，又是偶函数,所以选D.

7．C　函数y=x+sinx为非奇非偶函数，排除A、B、D．

8．C　考查三角函数的图象和性质.

由图可知=π.∴T=4π,∴ω==.

∴f(x)=sin(x+φ),将(π,1)代入可求φ=+2kπ(k∈Z).

9．2cosx　逆推，y=1-2sin²x=cos2x-y=cos2x,即y=-cos2xy=-cos［2(x+)］,即y=sin2x.

于是sin2x=f(x)sinx.∴f(x)是2cosx.

10．6　由题意1<<3,又k∈N*∴,∴k的最大值为6.

11．π　由图象的对称性，转化为图中一个长为π,宽为2的矩形的面积.

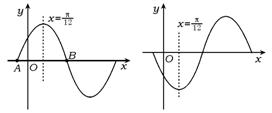12．①③②④;②③①④

①③成立时，f(x)的图象可能为图6中的一个.

但右图不能满足-<φ<.

图6

在图中可得端点A(-,0),B(,0),故②④成立.

同理②③成立时，①④成立.

13．周期为π　确定了一条对称轴和最高点的纵坐标后，如果不知周期性，还是不能确

定ω，解析式不能确定．

14．解　（1）当x∈［-, π］时，函数f(x)=Asin(ωx+φ)(A>0,ω>0,-<φ<),观察图象易得A=1,ω=1,φ=,即函数f(x)=sin(x+),由函数y=f(x)的图象关于直线x=-对称得x∈［-π,-］时，函数f(x)=-sinx.∴f(x)=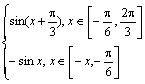

(2)当时，由sin(x+)=得x+=或x=-或x=;

当x∈［-π,-］时，由-sinx=得x=-或x=-.

∴方程f(x)=的解集为{-,-,-,).

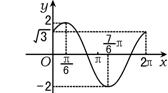15．解　如图7，在同一坐标系中画出y=2sin(θ+),y=m(θ∈R)的图象，由图可知，当-2<m<或<m<2时，直线与曲线有两个交点，即原方程有两个不同的实根.

当<m<2时，设原方程有一个根为x₁=+α，

则另一根为x₂=-α，∴x₁+x₂=.

图7

当-2<m<时，设原方程的一个根为x₁=π+α，

则另一个根为x₂=π-α.∴x₁+x₂=π.

16．解　f(x) =2cosxsin²x+sinx·cosx=sin2x+cos2x

=2

(1)最小正周期T=π;

(2)当且仅当2x+=2kπ-即x=kπ-π(k∈Z)时,f(x)_min=-2;

(3)据反函数性质，设f ^-1(1)=x₀,

∴1=2sin(2x₀+),sin(2x₀+)=

∵x₀∈，∴2x₀+=,∴x₀=,∴f ^-1(1)=.

点评　此题考查三角式的化简能力,三角函数性质及反函数的本质，此题有两个关键:一是有目的地化简，二是求f ^-1(1)的灵活性.

17．解　(1)x=cos²πt-2sinπtcosπt+sin²πt=1-sin²πt(-1≤t≤1)，其图象如图8①所示．

(2)由=cos²πt-sin²πt=cos²πt,得y=cos²2πt=1-sin²2πt．

由(1)知sin2πt=1-x (0≤x≤2)，∴y=1-(1-x)²=-x²+2x，

∴y=g(x)=-x²+2x (0≤x≤2)，其图象如图8②所示．

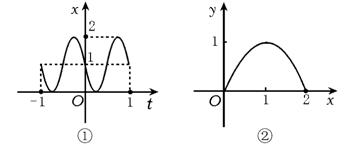		图8