![]() 高考文科数学2月联考试题
高考文科数学2月联考试题
数学(文)试题
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。共4页。全卷共150分。
第Ⅰ卷(选择题部分,共50分)
注意事项:
1、 答卷前,考生务必将自己的姓名、班级、学号填写在答题卡上。
2、 每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
一、选择题(本大题共10小题,每小题5分,共50分)
1、设集合![]() ,
,![]() ,则集合
,则集合![]() 中元素的个数为( ) A、0 B、1 C、2 D、3
中元素的个数为( ) A、0 B、1 C、2 D、3
2、 已知向量a =![]() ,向量b =
,向量b =![]() ,且a∥ (a
,且a∥ (a![]() b),则实数
b),则实数![]() 等于( )
等于( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
﹣1
D.
﹣1
3、在等差数列![]() 中,若
中,若![]() ,则此数列的前13项之和为( )
,则此数列的前13项之和为( )
(A)39 (B)52 (C)78 (D) 104
4、条件“![]() ”是条件“
”是条件“![]() ”的( )
”的( )
(A )充分非必要条件 (B )必要非充分条件
(C) 充分必要条件 (D) 既非充分也非必要条件
5、设![]() 、
、![]() 是不同的直线,
是不同的直线,![]() 、
、![]() 、
、![]() 是不同的平面,有以下四个命题:
是不同的平面,有以下四个命题:
①
若![]() 则
则![]() ②若
②若![]() ,
,![]() ,则
,则![]()
③
若![]() ,则
,则![]() ④若
④若![]() ,则
,则![]()
其中真命题的序号是( )
(A) ①④ (B) ②③ (C) ②④ (D) ①③
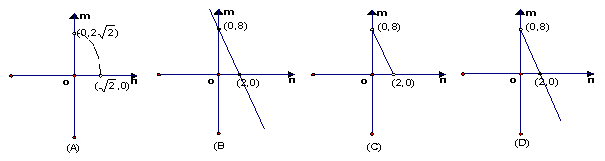
6、已知椭圆![]() 与双曲线
与双曲线![]() 有相同的准线,则动点
有相同的准线,则动点![]() 的轨迹为( )
的轨迹为( )
7、函数![]() )为增函数的区间是( )
)为增函数的区间是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
8、.已知直线![]() 与圆
与圆![]() 相交于A、B两点,且
相交于A、B两点,且![]() ,则
,则
![]() 的值为( )
的值为( )
( A)![]() ( B)
( B) ![]() ( C)
( C) ![]() (D)
(D) ![]()
9、在象棋比赛中,参赛的任意两位选手都比赛一场,其中胜者得2分,负者得0分,平局各得1分. 现有四名学生分别统计全部选手的总得分为131分,132分,133分,134分,但其中只有一名学生的统计结果是正确的,则参赛选手共有( )
(A)11位 ( B)12位 (C)13位 (D)14位
10、已知函数![]() 的定义域是
的定义域是![]()
![]() ,值域是
,值域是![]() ,那么满足条件的整数数对
,那么满足条件的整数数对![]() 共有( )
共有( )
(A)2个 (B)3个 (C) 5个 (D)无数个
二、填空题:本大题共5个小题,每小题5分,共25分,把答案填在题中的横线上。
11、 在![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() ,则
,则![]() _________ .
_________ .
12、 已知![]() 的展开式中共有5项,其中常数项为_______(用数字作答).
的展开式中共有5项,其中常数项为_______(用数字作答).
13、已知函数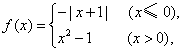 那么不等式
那么不等式![]() 的解集为
.
的解集为
.
14、有这样一种填数游戏:在![]() 的表格中,要求每个格子中都填上1、2、3三个数字中的某一个数字,且每一行和每一列都不能出现重复的数字,则此游戏共有_______种不同的填法
的表格中,要求每个格子中都填上1、2、3三个数字中的某一个数字,且每一行和每一列都不能出现重复的数字,则此游戏共有_______种不同的填法
15、已知![]() 、
、![]() 为不垂直的异面直线,
为不垂直的异面直线,![]() 是一个平面,则
是一个平面,则![]() 、
、![]() 在
在![]() 上的射影有可能是:①两条平行直线;②两条互相垂直的直线;③同一条直线;④一条直线及其外一点。在上面结论中,正确结论的编号是
上的射影有可能是:①两条平行直线;②两条互相垂直的直线;③同一条直线;④一条直线及其外一点。在上面结论中,正确结论的编号是
三.解答题:本大题共6小题,满分75分.解答应写出文字说明,证明过程或演算步骤.
16、(本题满分12分)A、B、C为△ABC的三个内角,且其对边分别为a、b、c.
若![]() =(-cos,sin),
=(-cos,sin),![]() =(cos,sin),且
=(cos,sin),且![]() ·
·![]() =
=
(1)求A;
(2)若a=2,三角形面积S=,求b+c的值.
17、(本题满分12分)如图,直二面角E-AB-C中,四边形ABEF是矩形,AB=2,AF=![]() ,ΔABC是以A为直角顶点的等腰直角三角形,点P是线段BF上的一个动点.
,ΔABC是以A为直角顶点的等腰直角三角形,点P是线段BF上的一个动点.
(1)若PB=PF,求异面直线PC与AB所成的角的余弦值;
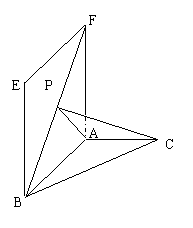 (2)若二面角P-AC-B的大小为300,求证:FB⊥平面PAC.
(2)若二面角P-AC-B的大小为300,求证:FB⊥平面PAC.
18、(本题满分12分)已知数列![]() 的前
的前![]() 项和为
项和为![]() ,又有数列
,又有数列![]() 满足关系
满足关系![]() ,对
,对![]() ,
,
有![]() ,
,![]()
(1) 求证:![]() 是等比数列,并写出它的通项公式;
是等比数列,并写出它的通项公式;
(2)
是否存在常数![]() ,使得数列
,使得数列![]() 为等比数列?若存在,求出
为等比数列?若存在,求出![]() 的值;若不存在,说明理由。
的值;若不存在,说明理由。
19、(本题满分12分)某工厂去年新开发的某产品的年产量为100万只,每只产品的销售价为10元,固定成本为8元.今年,工厂第一次投入100万元(科技成本),并计划以后每年比上一年多投入100万元(科技成本),预计产量年递增10万只,第n次投入后,每只产品的固定成本为![]() (k>0,k为常数,
(k>0,k为常数,![]() 且n≥0),若产品销售价保持不变,第n次投入后的年纯利润为
且n≥0),若产品销售价保持不变,第n次投入后的年纯利润为![]() 万元(年纯利润=年收入-年固定成本-年科技成本)
万元(年纯利润=年收入-年固定成本-年科技成本)
(1)求k的值,并求出![]() 的表达式;
的表达式;
(2)问从今年算起第几年纯利润最高?最高纯利润为多少万元?
20、(本小题满分13分) 已知函数![]()
(1)若函数![]() 在
在![]() 处有极值
处有极值![]() ,求
,求![]() 的单调递减区间;
的单调递减区间;
(2)若![]() 的导数
的导数![]() 对
对![]() 都有
都有![]() ,求
,求![]() 的取值范围。
的取值范围。
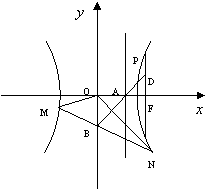
21、如图,已知双曲线![]() ,其右准线交x轴于点A, 双曲线虚轴的下端点为B.过双曲线的右焦点F
,其右准线交x轴于点A, 双曲线虚轴的下端点为B.过双曲线的右焦点F![]() 作垂直于x轴的直线交双曲线于点P,若点D满足
作垂直于x轴的直线交双曲线于点P,若点D满足![]() ,
,![]()
(1)求双曲线的离心率;
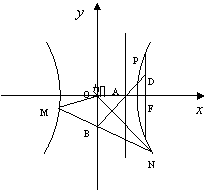 (2) 若
(2) 若![]() =2,过点B作直线
=2,过点B作直线![]() 分别交双曲线的左支、右支于M、N两点,且△OMN的面积
分别交双曲线的左支、右支于M、N两点,且△OMN的面积![]() =
=![]() ,
,
求![]() 的方程.
的方程.
高考文科数学2月联考试题
数学(文)试题 参考答案
一、选择题:![]()
二、填空题:
(11)![]() ① ② ④
① ② ④
16.解:(1)∵![]() =(-cos,sin),
=(-cos,sin),![]() =(cos,sin),且
=(cos,sin),且![]() ·
·![]() =,
=,
∴-cos2+sin2=,………………………………………………2分
即-cosA=,又A∈(0,p),∴A=p………………………………5分
(2)S△ABC=bc·sinA=b·c·sinp=![]() ,∴bc=4 …………………7分
,∴bc=4 …………………7分
又由余弦定理得:a2=b2+c2-2bc·cos120°=b2+c2+bc ………………10分
∴16=(b+c)2,故b+c=4.……………………………………………12分
17.解:(1)分别取BE、AB的中点M、N,
 连接PM、MC,PN、NC,则PM=1,MB=
连接PM、MC,PN、NC,则PM=1,MB=![]() ,BC=
,BC=![]() ,
,
∴MC=![]() ,而PN=MB=
,而PN=MB=![]() ,
,
NC=![]() ,∴PC=
,∴PC=![]() ,…………………………4分
,…………………………4分
∴![]()
故所求PC与AB所成角的余弦值为![]() ………6分
………6分
(2)连结AP,∵二面角E-AB-C是直二面角,且AC⊥AB
∴∠BAP即为所求二面角的平面角,即∠BAP=300……8分
在RtΔBAF中,tan∠ABF=![]() ,∴∠ABF=600,
,∴∠ABF=600,
故BF⊥AP, …………………………………………………………10分
又AC⊥面BF,∴BF⊥AC,故BF⊥平面PAC…………………………12分
(也可以用向量方法)
18、解:(1)由![]() ,又
,又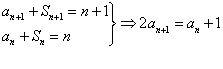 (3分)
(3分)
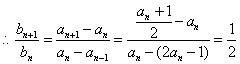 ,
,![]() 数列
数列![]() 为等比数列,且
为等比数列,且![]() (6分)
(6分)
(2)![]() (8分)
(8分)
![]() (10分)
(10分)
依题意,存在![]() ,使得数列
,使得数列![]() 为等比数列。 (12分)
为等比数列。 (12分)
19. 解:(1)由![]() ,当n=0时,由题意,可得k=8,
,当n=0时,由题意,可得k=8,
所以![]() .
……5分
.
……5分
(2)由![]()
![]()
![]() .
.
当且仅当![]()
![]() ,即n=8时取等号,所以第8年工厂的纯利润最高,
,即n=8时取等号,所以第8年工厂的纯利润最高,
最高为520万元 ……12分
20.解: (1)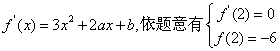 ………………………2分
………………………2分
即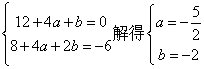
![]() ………4分
………4分
![]()
∴![]() 是
是![]() (也可写成闭区间)…………6分
(也可写成闭区间)…………6分
(2)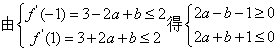 ……………………8分
……………………8分
不等式组所确定的平面区域如图所示。…………………………………10分
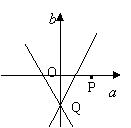
![]()
设
![]()
![]() ……………………………………13分
……………………………………13分
 21.(1)
21.(1)![]() B(0,-b)
B(0,-b)![]()
![]() ,即D为线段FP的中点.,
,即D为线段FP的中点.,
∴![]() ……………………………2分
……………………………2分
![]() ,即A、B、D共线.
,即A、B、D共线.
而 ![]()
![]()
∴![]() ,得
,得![]() ,………………………4分
,………………………4分
∴![]() ………………………………6分
………………………………6分
(2)∵![]() =2,而
=2,而![]() ,∴
,∴![]() ,
,
故双曲线的方程为![]() ………①………………………………7分
………①………………………………7分
∴B、的坐标为(0,-1)
设![]() 的方程为
的方程为![]() …………②
…………②
②代入①得![]()
由题意得: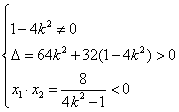 得:
得:![]() …………9分
…………9分
设M、N的坐标分别为(x1,y1) 、(x2,y2)
则![]()
而![]()
![]()
![]() ………12分
………12分
整理得![]() , 解得:
, 解得: ![]() 或
或![]() (舍去)
(舍去)
∴所求![]() 的方程为
的方程为![]() ………………………………14分
………………………………14分