高考数学串讲（二） 直线 平面 简单几何体
一，基础知识
1,直线,平面之间的平行与垂直的证明方法
（1）,运用定义证明(有时要用反证法); （2）,运用平行关系证明;
（3）,运用垂直关系证明; （4）,建立空间直角坐标系,运用空间向量证明
2,空间中的角和距离的计算
（1）,求异面直线所成的角
①,(平移法)过P作
,
,则
与
的夹角就是
与
的夹角;
②,证明
(或
),则与的夹角为
(或
);
③,求
与
所成的角(
),再化为异面直线与所成的角(
).
（2）,求直线与平面所成的角
①(定义法)若直线在平面
内的射影是直线,则与的夹角就是与的夹角;
②,证明
(或
),则与的夹角为(或);
③求与的法向量
所成的角
,则与所成的角为
或
.
（3）,求二面角
①,(直接计算)在二面角
的半平面内任取一点
,过P作AB的垂线,
交AB于C,再过P作
的垂线,垂足为D,连结CD,则
,故
为所求的二面角.
②,(面积射影定理)设二面角的大小为(
),平面内一个平面图形F
的面积为
,F在内的射影图形的面积为
,则
.(当为钝角时取“
”).
③,(异面直线上两点的距离公式):
,其中是二面角
的平面角,EA在半平面内且
于点A,BF在半平面内且FB
AB于B,而
,
,
.
④,(法向量法)平面的法向量
与平面的法向量
所成的角为,则所求的二面角为
(同类)或
(异类).
（4）,求异面直线的距离
①(定义法)求异面直线公垂线段的长;
②(体积法)转化为求几何体的高;
③(转化法)转化为求平行线面间的距离或平行平面间的距离;
④(最值法)构造异面直线上两点间距离的函数,然后求函数的最小值;
二，跟踪训练
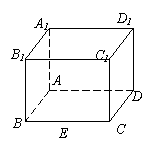1，（04湖北）如图，在棱长为1的正方体
中，点E是棱BC的中点，点F是棱CD上的动点。
（I）试确定点F的位置，使得
平面
；
（II）当平面时，求二面角
的大小（结果用反三角函数值表示）
2，（04北京）如图，在正三棱柱
中，
AB＝3，
，M为
的中点，P是BC上一
点，且由P沿棱柱侧面经过棱
到M的最短路线
长为
，设这条最短路线与的交点为N，求：
（I）该三棱柱的侧面展开图的对角线长；
（II）PC和NC的长；
（III）平面NMP与平面ABC所成二面角（锐角）的大小（用反三角函数表示）。
|
中，
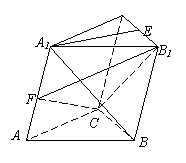
，AB=AC，
，侧面
与底面ABC所成的二面角为
，E，F分
别是棱
，
的中点。
（I）求与底面ABC所成的角；
（II）证明：
平面
；（III）求经过
，A，B，C四点的球的体积。
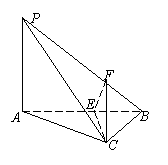
4，（05广东）如图，在四面体
中，已知PA=BC=6，
PC=AB=10，AC=8，PB=
。F是线段PB上一点，
CF=
，点E在线段AB上，且
。
（I）证明：
平面CEF；
（II）求二面角
的大小。
5，（05湖南）如图1，已知ABCD是上，下底边长分别
为2和6，高为
的等腰梯形，将它沿对称轴
折成直二面角，如图2。
（I）证明：
；
（II）求二面角
的大小。
三，简明提示
1，（I）设
，得
，当点F是CD的中点时，平面；
（II）二面角的大小为
。
2，（I）
；（II）
；（III）
。
3，（I）
；（II）略；（III）半径
，
。
4，（I）由勾股定理得
均为直角，得
平面ABC，
再用等面积法证明
，结合可证；
（II）
为所求的二面角的平面角，
。
5，（I）建立空间直角坐标系，可证得；（II）用法向量法可求得
。