高考数学串讲(五) 解三角形
一,基础知识

|
如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,外接圆
,外接圆
半径为R,内切圆半径为![]() ,半周长为
,半周长为![]() 。
。
(1)正弦定理:![]() 。
。
变形:![]() 。
。
(2)余弦定理:
![]() ;
;![]() ;
;![]() 。
。
(3)面积:![]() =
=![]() 。
。
2,等差数列与等比数列
(1),等差数列:
①,定义:![]() .
.
②,通项公式:![]() .
.
③,前![]() 项和公式:
项和公式:![]() .
.
④,任意两项![]() 有
有![]() .
.
⑤,对于任意正整数![]() ,若
,若![]() ,则
,则![]() .反之不行.
.反之不行.
⑥,若![]() 均是等差数列,则
均是等差数列,则![]() 也是等差数列.(
也是等差数列.(![]() )
)
(2),等比数列:
①,定义:![]() .
.
②,通项公式:![]() .
.
③,前![]() 项和公式:
项和公式: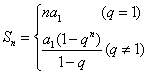 .④,任意两项
.④,任意两项![]() 有
有![]() .
.
⑤,对于任意正整数![]() ,若
,若![]() ,则
,则![]() .
.
⑥,无穷递缩等比数列所有项和公式:![]() .
.
二,跟踪训练
1,(05湖南)已知在![]() 中,
中,![]() ,
,![]() ,
,
求角A,B,C的大小。
2,(05湖北)在![]() 中,已知
中,已知![]() ,
,![]() ,AC边上的中线
,AC边上的中线
BD![]() ,求
,求![]() 的值。
的值。
3,(05天津)在![]() 中,
中,![]() 所对的边长分别为
所对的边长分别为![]() 。设
。设![]() 满足
满足
![]() 和
和![]() ,求
,求![]() 和
和![]() 的值。
的值。
4,(05全国III)![]() 中,内角A,B,C的对边分别为
中,内角A,B,C的对边分别为![]() ,已知
,已知![]() 成等比数列,
成等比数列,
且![]() 。
。
(I)求![]() 的值;
的值;
(II)设![]() ,求
,求![]() 的值。
的值。
5,(04广东)已知![]() 成公比为2的等比数列(
成公比为2的等比数列(![]() ),且
),且![]()
也成等比数列。求![]() 的值。
的值。
6,(04浙江)在![]() 中,角A,B,C的对边分别为
中,角A,B,C的对边分别为![]() ,且
,且![]() 。
。
(I)求![]() 的值;
的值;
(II)若![]() ,求
,求![]() 的最大值。
的最大值。
7,(04北京)在![]() 中,
中,![]() ,AC=2,AB=3,求
,AC=2,AB=3,求![]() 的值和
的值和
![]() 的面积。
的面积。
8,(04全国II)已知锐角![]() 中,
中,![]() ,
,![]() 。
。
(I)求证:![]() ;
;
(II)设AB=3,求AB边上的高。
三,简明提示
1,由![]() 得
得![]() ,有
,有
![]() ,得
,得![]() ,由
,由![]() 得
得
![]() ,有
,有![]() ,得
,得![]() 。
。
2,设E为BC的中点,连结DE,则DE//AB,且![]() ,设
,设![]() ,有
,有
![]() ,得
,得![]() 或
或![]() (舍去),有BC=2。
(舍去),有BC=2。
从而![]() =
=![]() ,得
,得![]() 。
。
又![]() ,而
,而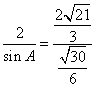 ,于是
,于是![]() 。
。
3,由题设条件,应用两角差的正弦公式得
![]() ,即
,即![]() ①
①
由题设条件,应用二倍角余弦公式得
![]()
故![]() ②
②
由①和②式得![]() ,
,![]()
![]()
因此,![]() ,由两角和的正切公式
,由两角和的正切公式
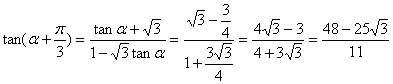
4,(I)由![]() 得
得![]() ,由
,由![]() 得
得![]() 于是
于是
![]() 。
。
(II)由![]() ,得
,得![]() ,由
,由![]() ,得
,得![]() ,即
,即![]() 。
。
又![]() 。得
。得![]() ,
,![]() ,得
,得![]() 。
。
5,解:∵α,β,γ成公比为2的等比数列,∴β=2α,γ=4α
∵sinα,sinβ,sinγ成等比数列
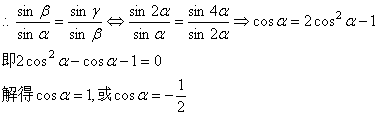
当cosα=1时,sinα=0,与等比数列的首项不为零,故cosα=1应舍去,
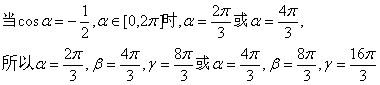
6,解:(I)![]()
= ![]() =
= ![]() 。
。
(II)由![]() ,得
,得![]() ,有
,有![]() 。
。
又![]() ,得
,得![]() ,当且仅当
,当且仅当![]() 时,
时,![]() 的最大值是
的最大值是![]() 。
。
7,解:![]()
![]() 。
。
又![]() ,
,![]()
![]()
![]()
![]()
8,(Ⅰ)证明:![]()
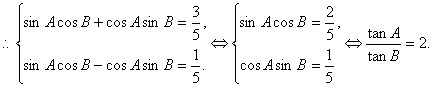
所以![]()
(Ⅱ)解:![]() ,
,![]()
即![]() ,将
,将![]() 代入上式并整理得
代入上式并整理得
![]()
解得![]() ,舍去负值得
,舍去负值得![]() ,
,
![]() 设AB边上的高为CD.
设AB边上的高为CD.
则AB=AD+DB=![]()
由AB=3,得CD=2+![]() . 所以AB边上的高等于2+
. 所以AB边上的高等于2+![]() .
.