08年高三理科数学测试题
![]()
![]() 命题:覃明富 孙红波 王圣忠 审题:杨天文 王圣忠
2008.2.23
命题:覃明富 孙红波 王圣忠 审题:杨天文 王圣忠
2008.2.23
满分150分。考试用时120分钟。
注意事项:
1. 答题前,考生务必将自己的姓名、考号填在试卷的答题卡上。
2. 选择题务必用2B铅笔填涂,解答题必须使用黑色墨水的签字笔作答;字迹工整,笔迹清晰。
3. 请在答题区域内作答,超出答题区域黑色边框的答案无效。
一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知![]() ,则
,则![]() 等于( )
等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.![]() =( )
=( )
A.![]() B.0 C.
B.0 C.![]() D.
D.![]()
3.若![]() ,则
,则![]() 的值为 (
)
的值为 (
)
A. ![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.已知向量![]() ,
,![]() (1,
(1, ![]() ),则
),则![]() 的最小值是( )
的最小值是( )
A.1 B.![]() C.
C.![]() D.2
D.2
5.已知数列![]() 为等差数列,且
为等差数列,且![]() ,则
,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.已知p:![]() ,q:
,q:![]() ,若
,若![]() 是
是![]() 的充分条件,则
的充分条件,则![]() 的取值范围为( )
的取值范围为( )
A. ![]() B.
B.![]() C.
C.![]() 或
或![]() D.
D.![]() 或
或![]()
7.关于直线![]() ,
,![]() 与平面
与平面![]() ,
,![]() ,有以下四个命题:
,有以下四个命题:
①若![]() 且
且![]() ,则
,则![]() ; ②若
; ②若![]() 且
且![]() ,则
,则![]() ;
;
③若![]() 且
且![]() ,则
,则![]() ; ④若
; ④若![]() 且
且![]() ,则
,则![]() .
.
其中真命题的序号是 ( )
A.①② B.③④ C.①④ D.②③
8.把函数![]() 的图象沿
的图象沿![]() 轴平移
轴平移![]() 个单位,所得图象关于原点对称,则
个单位,所得图象关于原点对称,则![]() 的最小值是( )
的最小值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.过双曲线M:![]()
![]() 的左顶点A作斜率为1的直线
的左顶点A作斜率为1的直线![]() ,若
,若![]() 与双曲线M的两条渐近线分别相交于B、C,且AB=BC,则双曲线M的离心率是( )
与双曲线M的两条渐近线分别相交于B、C,且AB=BC,则双曲线M的离心率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
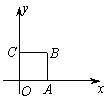 10.如图,在平面直角坐标系
10.如图,在平面直角坐标系![]() 中,
中,![]() ,映
,映
射![]() 将
将![]() 平面上的点
平面上的点![]() 对应到另一个平面直角坐标系
对应到另一个平面直角坐标系
![]() 上的点
上的点![]() ,则当点
,则当点![]() 沿着折线
沿着折线![]() 运
运
动时,在映射![]() 的作用下,动点
的作用下,动点![]() 的轨迹是( )
的轨迹是( )
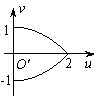
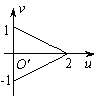
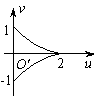
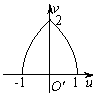
A. B. C. D.
二、填空题:本大题共5小题,每小题5分,共25分,把答案填写在答题卡的相应位置11.![]()
12. 设中心在原点的双曲线与椭圆
设中心在原点的双曲线与椭圆![]()
![]() =1有公共的焦点,且它们的离心率互为倒数,则该双曲线的方程是
=1有公共的焦点,且它们的离心率互为倒数,则该双曲线的方程是
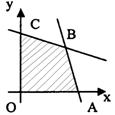
13.如图,目标函数![]() 的可行域为四边形
的可行域为四边形![]() (含边界),
(含边界),
![]() 、
、![]() ,若
,若![]() 为目标函数取最大值的最优解,则
为目标函数取最大值的最优解,则
![]() 的取值范围是
的取值范围是
14.把正方形ABCD沿对角线AC折起,构成以A、B C、D四点为顶点的三棱锥,当点D到平面ABC的距离最大时,直线BD与平面ABC所成的角的大小为
15.关于函数 (
(![]() 为常数,且
为常数,且![]() )对于下列命题:①函数
)对于下列命题:①函数![]() 的最小值为-1;②函数
的最小值为-1;②函数![]() 在每一点处都连续;③函数
在每一点处都连续;③函数![]() 在R上存在反函数;④函数
在R上存在反函数;④函数![]() 在
在![]() 处可导;⑤对任意的实数
处可导;⑤对任意的实数![]() 且
且![]() ,恒有
,恒有![]()
其中正确命题的序号是___________________。
三、解答题:本大题共6小题,共75分,解答应写出文字说明、证明过程或演算步骤
16.(本题满分12分)已知向量![]()
![]() 已知角
已知角![]() 的终边上一点
的终边上一点![]() ,记
,记![]() 。
。
⑴求函数![]() 的最大值,最小正周期;
的最大值,最小正周期;
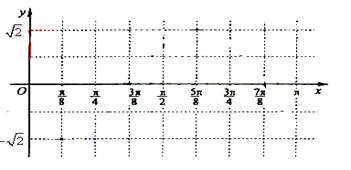
⑵作出函数![]() 在区间[0,π]上的图象。
在区间[0,π]上的图象。
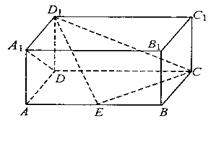 17.(本题满分12分)如图,在长方体ABCD—A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.
17.(本题满分12分)如图,在长方体ABCD—A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.
(1)证明:D1E⊥A1D;
(2)当E为AB的中点时,求点A到面ECD1的距离;
(3)AE等于何值时,二面角D1—EC—D的大小为![]() .
.
18.(本小题满分12分)随着机构改革的深入进行,各单位要减员增效,有一家公司现有职员2a人(140<2a<420,且a为偶数![]() ,每人每年可创利b万元. 据评估,在经营条件不变的前提下,每裁员1人,则留岗职员每人每年多创利0.01b万元,但公司需付下岗职员每人每年0.4b万元的生活费,并且该公司正常运转所需人数不得小于现有职员的
,每人每年可创利b万元. 据评估,在经营条件不变的前提下,每裁员1人,则留岗职员每人每年多创利0.01b万元,但公司需付下岗职员每人每年0.4b万元的生活费,并且该公司正常运转所需人数不得小于现有职员的![]() ,为获得最大的经济效益,该公司应裁员多少人?
,为获得最大的经济效益,该公司应裁员多少人?
19.(本题满分12分)已知数列![]() 的首项
的首项![]() ,前
,前![]() 项和为
项和为![]() ,且
,且![]() 、
、![]() 、
、![]() 分别是直线
分别是直线![]() 上的点A、B、C的横坐标,点B分
上的点A、B、C的横坐标,点B分![]() 所成的比为
所成的比为![]() ,设
,设![]()
![]() 。
。
⑴ 判断数列![]() 是否为等比数列,并证明你的结论;
是否为等比数列,并证明你的结论;
⑵ 设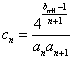 ,证明:
,证明:![]() 。
。
20.(本题满分13分)已知半圆![]() ,动圆
,动圆![]() 与此半圆相切且与
与此半圆相切且与![]() 轴相切。
轴相切。
(1)求动圆圆心![]() 的轨迹方程。
的轨迹方程。
(2)是否存在斜率为![]() 的直线
的直线![]() ,它与(1)中所得轨迹由左到右顺次交于A、B、C、D四个不同的点,且满足AD=2BC?若存在,求出
,它与(1)中所得轨迹由左到右顺次交于A、B、C、D四个不同的点,且满足AD=2BC?若存在,求出![]() 的方程,若不存在,说明理由。
的方程,若不存在,说明理由。
21.(本题满分14分)对于函数![]() ,若存在
,若存在![]() ,使
,使![]() 成立,则称
成立,则称![]() 为
为![]() 的不动点。如果函数
的不动点。如果函数![]() 有且仅有两个不动点
有且仅有两个不动点![]() 、
、![]() ,且
,且![]() 。
。
(1)试求函数![]() 的单调区间;
的单调区间;
(2)已知各项不为零的数列![]() 满足
满足![]() ,求证:
,求证:![]() ;
;
(3)设![]() ,
,![]() 为数列
为数列![]() 的前
的前![]() 项和,求证:
项和,求证:![]() 。
。
宜昌市三校联合体2008届高三二月统考
数学(理科)试题 参考答案
1——10 BDCBA BDBAA
11.
![]() 12.
12.![]() 13.
13.![]() 14.
14.![]() 15.①②⑤
15.①②⑤
16.解:⑴角![]() 的终边上一点
的终边上一点![]()
![]() ……………2分
……………2分
![]()
![]()
![]() ……………6分
……………6分
![]() 的最大值为
的最大值为![]() , 最小正周期
, 最小正周期![]() ……………8分
……………8分
⑵略。……………12分
17.(1)证明:连![]() ,在长方体ABCD—A1B1C1D1中,
,在长方体ABCD—A1B1C1D1中,![]() 为
为![]() 在平面
在平面![]() 的射影,
的射影,
而AD=AA1=1,则四边形![]() 是正方形
是正方形![]() ,
,
由三垂线定理得D1E⊥A1D ……………3分
(2)解:以点D为原点,DA为![]() 轴,DC为
轴,DC为![]() 轴建立如图所示的直角坐标系。则
轴建立如图所示的直角坐标系。则![]()
![]() 、
、![]() 、
、![]() 、
、![]() 则
则![]() ,
,![]() ,
,
![]() ,设平面
,设平面![]() 的法向量为
的法向量为![]()
![]()
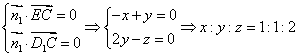 ,记
,记![]()
![]() 点A到面ECD1的距离
点A到面ECD1的距离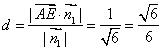 ……………7分
……………7分
(3)解:设![]() 则
则![]() ,设平面
,设平面![]() 的法向量为
的法向量为![]()
![]()
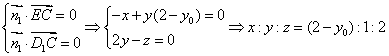 ,记
,记![]()
而平面ECD的法向量![]() ,则二面角D1—EC—D的平面角
,则二面角D1—EC—D的平面角![]()
![]()
 。
。
![]() 当AE=
当AE=![]() 时,二面角D1—EC—D的大小为
时,二面角D1—EC—D的大小为![]() 。……………12分
。……………12分
18.解:设裁员x人,可获得的经济效益为y万元,则
![]() ……………4分
……………4分
依题意
![]() ……………6分
……………6分
(1)当![]() 取到最大值;……………8分
取到最大值;……………8分
(2)当![]() 取到最大值;……………10分
取到最大值;……………10分
答:当![]() ,
,![]() ……………12分
……………12分
19.⑴由题意得![]() ……………3分
……………3分
![]()
![]()
![]() 数列
数列![]() 是以
是以![]() 为首项,以2为公比的等比数列。………………6分
为首项,以2为公比的等比数列。………………6分
[则![]()
![]()
![]() (
(![]() )]
)]
⑵由![]() 及
及![]() 得
得![]()
![]()
![]() ,……………………………………………………………8分
,……………………………………………………………8分
则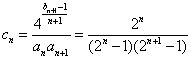
![]() ……………………10分
……………………10分
![]()
![]() ………………12分
………………12分
20.(1)设动圆圆心![]() ,作
,作![]() ⊥
⊥![]() 轴于点
轴于点![]()
①若两圆外切: ![]() ,则
,则![]() 化简得:
化简得:
![]()
![]()
![]()
![]() ……………3分
……………3分
 ②若两圆内切:
②若两圆内切: ![]() ,则
,则![]()
![]()
![]()
![]()
![]()
![]() ……………5分
……………5分
综上,动圆圆心的轨迹方程是
![]()
![]() 及
及![]()
![]() ……………6分
……………6分
其图象为两条抛物线位于![]() 轴上方的部分,如图所示。
轴上方的部分,如图所示。
(2)假设直线![]() 存在,可设
存在,可设![]() 的方程为
的方程为![]()
![]()
![]() 。
。
|
|
![]()
![]() 即
即
![]() ①
①
![]() ②
②
![]()
![]()
![]() ,
, ![]()
![]()
![]()
![]()
![]() 2
2![]()
![]()
![]() =2
=2![]()
即![]() +
+![]()
![]() =4
=4![]()
![]() -
-![]()
![]() 得
得![]()
![]() ……………11分
……………11分
将其代入方程①得 ![]()
![]()
![]()
因为曲线![]() 的横坐标范围为
的横坐标范围为![]() ,所以这样的直线
,所以这样的直线![]() 不存在。
不存在。
……………13分
21.(1)设![]()
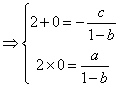 ∴
∴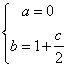 ∴
∴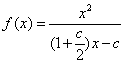
由![]()
又∵![]() ∴
∴![]()
∴![]() …… 3分
…… 3分
于是![]()
由![]() 得
得![]() 或
或![]() ; 由
; 由![]() 得
得![]() 或
或![]()
故函数![]() 的单调递增区间为
的单调递增区间为![]() 和
和![]() ,
,
单调减区间为![]() 和
和![]() ……4分
……4分
(2)由已知可得![]() , 当
, 当![]() 时,
时,![]()
两式相减得![]()
∴![]() 或
或![]()
当![]() 时,
时,![]() ,若
,若![]() ,则
,则![]() 这与
这与![]() 矛盾
矛盾
∴![]() ∴
∴![]() ……6分
……6分
于是,待证不等式即为![]() 。
。
为此,我们考虑证明不等式![]()
令![]() 则
则![]() ,
,![]()
再令![]() ,
,![]() 由
由![]() 知
知![]()
∴当![]() 时,
时,![]() 单调递增 ∴
单调递增 ∴![]() 于是
于是![]()
即![]() ①
①
令![]() ,
,![]() 由
由![]() 知
知![]()
∴当![]() 时,
时,![]() 单调递增 ∴
单调递增 ∴![]() 于是
于是![]()
即![]() ②
②
由①、②可知![]() ……10分
……10分
所以,![]() ,即
,即![]() ……11分
……11分
(3)由(2)可知![]() 则
则![]()
在![]() 中令
中令![]() ,并将各式相加得
,并将各式相加得
![]()
即![]() ……14分
……14分
