高考数学复习阶段测试试题

2008.3

一、填空题（本题共14小题，每小题5分，共70分）

1. 函数的定义域为 　　　 ▲　　　　  .

2.若命题“，使得”是真命题，则实数的取值范围为　

　　▲　 .

3. 一个空间几何体的主视图、左视图、俯视图为直角三角形，边长如图所示，那么这个几何体的体积为 　　　 ▲　　　 .

4.已知是偶函数，定义域为，则的值为　 ▲　　 .

5.在等差数列{}中，则

　　　▲　　　.　　　　　　 

6. 已知且，则复数对应点在第二象限的概率为

▲　　　　（用最简分数表示）

7. 直线与曲线相切于点，则b的值为　　　 ▲　　　　  .

8. 如果执行下面的程序框图，那么输出的等于　 ▲　　　.

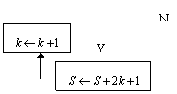9.在吸烟与患肺病这两个分类变量的计算中，“若的观测值为6.635，我们有99%的把握认为吸烟与患肺病有关系”这句话的意思：

①是指“在100个吸烟的人中，必有99个人患肺病

②是指“有1%的可能性认为推理出现错误”；

③是指“某人吸烟，那么他有99%的可能性患有肺病”；

④是指“某人吸烟，如果他患有肺病，那么99%是因为吸烟”。

其中正确的解释是　　　　　　　　　

10. 已知圆和直线交于A,B两点,O是坐标原点, 若,则　　 ▲　　　　.

11、已知实数x,y满足条件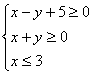，为虚数单位），则的最大值和最小值分别是　　　▲　　　　　 ．

12.当时，函数的最小值为　　　　▲　　.

13.将半径为1的圆周十二等分，从分点i到分点i+1的向量依次记作，　　　▲　　　　

14．已知，且方程无实数根，下列命题：

①方程也一定没有实数根；

②若，则不等式对一切实数都成立；

③若，则必存在实数，使

④若，则不等式对一切实数都成立．

中，正确命题的序号是 　　▲　 　．(把你认为正确的命题的所有序号都填上)

二、解答题：(本大题共6小题，共计90分．)

15．（ 14分）已知，点P的坐标为

（I）求当时，P满足的概率；

（II）求当时，P满足的概率．

16、（14分）如图，在正方体ABCD－A₁B₁C₁D₁中，E、F为棱AD、AB的中点．

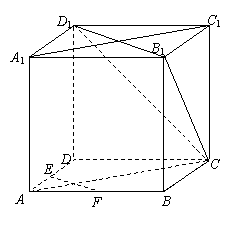（1）求证：EF∥平面CB₁D₁；

（2）求证：平面CAA₁C₁⊥平面CB₁D₁．　　　　　　　　

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

17、（15分）在△ABC中，角A、B、C的对边分别为a、b、c.已知a+b=5，c =，

且

(1) 求角C的大小；　　（2）求△ABC的面积.

18. （15分）如图，已知A、B、C是长轴长为4　 的椭圆上的三点，点A是长轴的右顶点，BC过椭圆中心O，且·=0，，

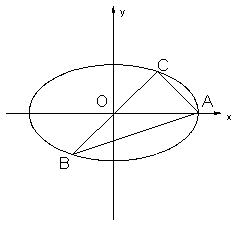（1）求椭圆的方程；

（2）若过C关于y轴对称的点D作椭圆的切线DE，则AB与DE有什么位置关系？证明你的结论.

19．（ 16分）设函数

（I）证明函数在上是单调增函数；

（II）若不等式，当时恒成立，求实数m的取值范围．

20．（ 16分）已知正项等差数列的前n项和为，其中都是数列中满足的任意项．

（I）证明：；

（II）证明：；

（III）若也在等差数列，且，求数列的前n项和．

参考答案

1. 　2. >3或<-1　3.　1  4.　　5.　15  6.　　7.　3  8. 441

9.　②　 10. 　11. 　12.　4  13.  14. ①②④

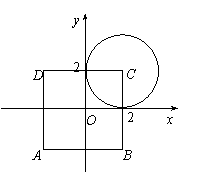15．（1）如图，点P所在的区域为正方形ABCD的内部（含边界），满足 的点的区域为以为圆心，2为半径的圆面（含边界）．

所求的概率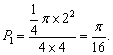　　　　　  ……………7分

（2）满足，且的点有25个，

满足，且的点有6个，

所求的概率　　　　　　　  ……………14分

16. （1）证明:连结BD. 在长方体中，对角线.

又 E、F为棱AD、AB的中点，. .

又B₁D₁平面，平面，

　EF∥平面CB₁D₁.　　　　　　　　　　　　　　　　 …………7分

（2） 在长方体中，AA₁⊥平面A₁B₁C₁D₁，而B₁D₁平面A₁B₁C₁D₁，

 AA₁⊥B₁D₁.

又在正方形A₁B₁C₁D₁中，A₁C₁⊥B₁D₁，

 B₁D₁⊥平面CAA₁C₁.　　　　　　　　 

又 B₁D₁平面CB₁D₁，

平面CAA₁C₁⊥平面CB₁D₁  …………14分

17.．(1) 解：∵A+B+C=180°

　　由　　　 …………2分

　　∴　　　　　　　　　　  ………………4分

　　整理，得　解 得：　　　　……6分

　　∵　∴C=60°　　　　　　　　　　　  ………………7分

（2）解：由余弦定理得：c²=a²+b²－2abcosC，即7=a²+b²－ab　　…………8分

∴　

由条件a+b=5得 7=25－3ab　　 　　　　　　　　　　　……12分

∴　　　　　　　　 …………15分

18. （1）A（2，0），设所求椭圆的方程为：=1(0<b<2) ，　　 ……2分

由椭圆的对称性知，OC=OB，由·=0得，AC⊥BC，

∵BC=2AC，∴OC=AC，∴△AOC是等腰直角三角形，

∴C的坐标为（1，1）．　　　　　　　　　　　　　　　　 　　　……4分

∵C点在椭圆上，∴=1，∴b²=．

所求的椭圆方程为=1．　　　　　　　　　　　　　　　 ……8分

（2）是平行关系.…………10分

D（-1，1），设所求切线方程为y-1=k（x+1）

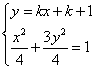，消去x， …………12分

上述方程中判别式=，

又，所以AB与DE平行.　　　　　　　　　　　　  …………15分

19．（I），

当时，在上是单调增函数．　　…………7分

（II），

原不等式即为在时恒成立．

的最大值为1，在时恒成立．

令，则，且

由，解得或

由，解得或

综上得，或　　　　　　　　　　　　　　　　  …………16分

20．（I）设数列的公差为d，由题意

　　　　  …………4分

（II）

　　　　　　　　　　

　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　 …………9分

（III）取，显然满足

由也成等差数列，则

两边平方得，

再两边平方整理得，即

，显然这时数列满足题意．

设数列的前n项和为，

则

　　　　　　　　　　　　　　　 …………16分