08届高考理科数学第一次模拟问卷
★★理科数学★★ 2008-2-20上午
一、选择题:本大题共分8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合![]() ,
,![]() ,则集合
,则集合![]() ( )
( )
A. ![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.数列![]() ,……的前n项和为 ( )
,……的前n项和为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.已知![]() ,则
,则![]() 的值为 ( )
的值为 ( )
A. 1 B.![]() C.
C.![]() D.2
D.2
4.若函数![]() 的最小正周期为1,则它的图象的一个对称中心为( )
的最小正周期为1,则它的图象的一个对称中心为( )
A (![]() B (
B (![]() )
) ![]() C (
C (![]() ) D (0,0)
) D (0,0)
5.已知函数![]() 等于 ( )
等于 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.设等差数列![]() 的前n项和是
的前n项和是![]() 且
且![]() ,则
( )
,则
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
7.偶函数![]() 满足:
满足:![]() ,且在区间[0,3]与
,且在区间[0,3]与![]() 上分别递减和递增,则不等式
上分别递减和递增,则不等式![]() 的解集为
( )
的解集为
( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
8.定义在![]() 上的函数
上的函数![]() 的图象关于点
的图象关于点![]() 成中心对称,对任意的实数
成中心对称,对任意的实数![]() 都有
都有![]() ,且
,且![]()
![]() ,则f(1)+f(2)+f(3)+······+f(2008)的值为( )
,则f(1)+f(2)+f(3)+······+f(2008)的值为( )
A.![]() B.
B.![]() C.0 D.1
C.0 D.1
 二、填空题:本大题共7小题,每小题5分,满分30分.其中13~15题是选做题,考生只能选做二题,三题全答的,只计算前两题得分.
二、填空题:本大题共7小题,每小题5分,满分30分.其中13~15题是选做题,考生只能选做二题,三题全答的,只计算前两题得分.
9.函数![]() 的定义域是_______________.
的定义域是_______________.
10.设直线![]() 过椭圆的左焦点F和一个顶点B(如图所示),
过椭圆的左焦点F和一个顶点B(如图所示),
则这个椭圆的离心率![]() __________.
__________.
11.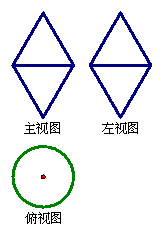 如右图,一个空间几何体的主视图、左视图是周长为4一个内角为
如右图,一个空间几何体的主视图、左视图是周长为4一个内角为![]() 的菱形,俯视图是圆及其圆心,那么这个几何体的表面积为________.
的菱形,俯视图是圆及其圆心,那么这个几何体的表面积为________.
12.设平面![]() ∩平面
∩平面![]() ,点
,点![]() 平面
平面![]() ,点
,点![]() 平面
平面![]() ,且三点A、B、C都不在直线l上,给出下列四个命题:
,且三点A、B、C都不在直线l上,给出下列四个命题:
① ![]() ②
② ![]()
③ ![]() 平面ABC. 其中正确的命题是_______________.
平面ABC. 其中正确的命题是_______________.
(从下列13~15三小题中任选做两小题,如果三小题都做的,则只按前两小题记分)
 13.如图所示,AC和AB分别是圆O的切线,
且OC = 3,AB = 4,延长OA到D点,则
13.如图所示,AC和AB分别是圆O的切线,
且OC = 3,AB = 4,延长OA到D点,则
△ABD的面积是___________.
14.在极坐标系中,点![]() 到
到![]()
的距离是___________.
15. 已知g(x)=x-1-x-2,则g(x)的值域为 ;
班级 姓名 学号 得分
一、选择题:本大题共分8小题,每小题5分,共40分。
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 答案 |
|
|
|
|
|
|
|
|
二、填空题:本大题共7小题,每小题5分,满分30分.其中13~15题是选做题,考生只能选做二题,三题全答的,只计算前两题得分.
9. ; 10. ;
11. ; 12. ;
(从下列13~15三小题中任选做两小题,如果三小题都做的,则只按前两小题记分)
13. ; 14. ; 15. .
三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.
16.(本小题满分12分)
在△ABC中,角A、B、C的对边分别为a、b、c.已知a+b=5,c =![]() ,且
,且![]() (1) 求角C的大小; (2)求△ABC的面积.
(1) 求角C的大小; (2)求△ABC的面积.
17.(本小题满分12分)
一位学生每天骑车上学,从他家到学校共由5个交通岗,假设他在每个交通岗遇到红灯是相互独立的,且首末两个交通岗遇红灯的概率均为P,其余3个交通岗遇红灯的概率为![]() 。
。
(1)若![]() ,求该学生在第三个交通岗第一次遇到红灯的概率;
,求该学生在第三个交通岗第一次遇到红灯的概率;
(2)若该学生至多遇到一次红灯的概率不超过![]() ,求P。
,求P。
理科数学
班级 姓名 学号 得分
18.(本小题满分14分)
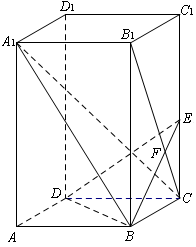 如图,已知正四棱柱ABCD—A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,过点B作B1C的垂线交侧棱CC1于点E,交B1C于点F,
如图,已知正四棱柱ABCD—A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,过点B作B1C的垂线交侧棱CC1于点E,交B1C于点F,
(1)求证:A1C⊥平面BDE;
(2)求A1B与平面BDE所成角的正弦值;
(3)设F是CC1上的动点(不包括端点C),
求证:△DBF是锐角三角形。
19.(本小题满分14分)
在等差数列{an}中,a1=1,前n项和Sn满足条件![]() (n为正整数)。
(n为正整数)。
(1) 求等差数列{an}的通项公式;
(2)
记![]() ,求数列{bn}的前n项和
,求数列{bn}的前n项和![]() 。
。
20.(本小题满分14分)
函数![]() 函数f(x)当x=1时有极值。
函数f(x)当x=1时有极值。
(1) 求m与n的关系表达式;
(2) 求f(x)的单调区间;
(3)
当![]() 函数y=f(x)的图象上任意一点的切线斜率恒大于3m,求m的取值范围。
函数y=f(x)的图象上任意一点的切线斜率恒大于3m,求m的取值范围。
21.(本小题满分14分)
已知中心在原点的双曲线C的右焦点为(2,0),右顶点为![]()
(1)求双曲线C的方程;
(2)若直线![]() 与双曲线C恒有两个不同的交点A和B,且
与双曲线C恒有两个不同的交点A和B,且![]()
(其中O为原点). 求k的取值范围.
理科数学(答案)
一、 选择题 ACAC BBDC
二、
填空题 9.(-2,2); 10. ![]() ; 11.π
; 12.②③
;
; 11.π
; 12.②③
;
13. ![]() ;
14. 1 ; 15.[-1,1]
;
14. 1 ; 15.[-1,1]
三、解答题:
16.(本小题满分12分)
(1) 解:∵A+B+C=180°
由![]() …………1分
…………1分
∴![]() ………………3分
………………3分
整理,得![]() …………4分
…………4分
解 得:![]() ……5分
……5分
∵![]() ∴C=60° ………………6分
∴C=60° ………………6分
(2)解:由余弦定理得:c2=a2+b2-2abcosC,即7=a2+b2-ab …………7分
∴![]() ………………8分
………………8分
由条件a+b=5得 7=25-3ab …… 9分
![]() ……10分
……10分
∴![]() …………12分
…………12分
17. 解:(1)记该学生在第![]() 个交通岗遇到红灯事件为
个交通岗遇到红灯事件为![]() 他们相互独立,则这名学生在第三个交通岗第一次遇到红灯为
他们相互独立,则这名学生在第三个交通岗第一次遇到红灯为![]()
P(![]() )=
)=![]()
这名学生在第三个交通岗第一次遇到红灯为![]() 。
。
(2)过首末两个路口,共中间三个路口分别看作独立重复试验,
A={该学生没遇到红灯} B={该学生恰好遇到一次红灯},则A与B互斥
![]()

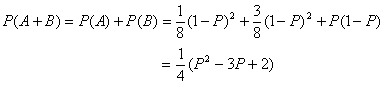
故![]()
![]()
18. (1)证明:由正四棱柱性质知A1B1⊥平面BCC1B1,A1A⊥平面ABCD,
所以B1C、AC分别是A1C在平面CC1B1B、平面ABCD上的射影
∵ B1C⊥BE, AC⊥BD, ∴A1C⊥BE , A1C⊥BD, (2分)
∴ A1C⊥平面BDE (4分)。 (直接指出根据三垂线定理得“A1C⊥BE , A1C⊥BD”而推出结论的不扣分)
(2)解:以DA、DC、DD1所在直线分别为x、y、z轴,建立坐标系,则![]() ,
,![]() ,
,![]() ,∴
,∴![]() ,
,![]() (6分)
(6分)
∴ (7分)
(7分)
设A1C![]() 平面BDE=K,
平面BDE=K,
由(1)可知,∠A1BK为A1B与平面BDE所成角,(8分)
∴![]() (9分)
(9分)
(1)
证明:设点F的坐标为(0, 2, z)(0<z≤4), 则![]() ,
,
又DB=![]() ,故△DBF是等腰三角形,要证明它为锐角三角形,只需证明其顶角∠DFB为锐角则可。
(11分)
,故△DBF是等腰三角形,要证明它为锐角三角形,只需证明其顶角∠DFB为锐角则可。
(11分)
由余弦定理得cos∠DFB=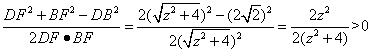
∴∠DFB为锐角, (13分)
即不论点F为CC1上C点除外的任意一点, △DFB总是锐角三角形.(14分)
说明: 若没有说明三角形为等腰三角形而只证明一个角是锐角,或只证明底角是锐角的“以偏概全”情况应扣2分)
19、解:![]() (1)
(1)![]() an=n
…….4分
an=n
…….4分
(2)Tn=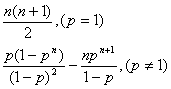 …….14分
…….14分
20、解:(1)n=3m+6…….4分
(2) ![]() …….14分
…….14分
21. 解:(Ⅰ)设双曲线方程为![]()
![]()
由已知得![]()
故双曲线C的方程为![]()
(Ⅱ)将![]()
![]()
由直线l与双曲线交于不同的两点得
即![]() ① 设
① 设![]() ,则
,则
![]()
而![]()
![]()
于是![]()
![]() ②
②
由①、②得 ![]()
故k的取值范围为![]()
