08届高考理科数学第二次模拟问卷
理科问卷
一.选择题:本大题共8小题。在每小题给出的四个选项中,只有一项是符合题目要求的.每小题5分,满分40分.
 1.已知集合
1.已知集合![]() ,
,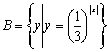 ,则
,则
A ![]() B
B ![]() C
C ![]() D
D ![]()
2、4.已知![]() 是等差数列,
是等差数列,![]() ,其前10项和
,其前10项和![]() ,
,
则其公差![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3、函数![]() 在区间A是增函数,则区间A为( )
在区间A是增函数,则区间A为( )
A、(-∞,0]
B、[0,+∞)C、[0,![]() ] D、(
] D、(![]() ,+∞)
,+∞)
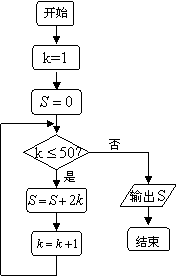
4、如果执行的程序框图(右图所示),那么输出的![]() ( ).
( ).
A.2450 B.2500 C.2550 D.2652
5、曲线![]() 在点
在点![]() 处的切线与坐标轴所围三角形的面积
处的切线与坐标轴所围三角形的面积
为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.定义运算a![]() b=
b=![]() ,则函数f(x)=1
,则函数f(x)=1![]() 2
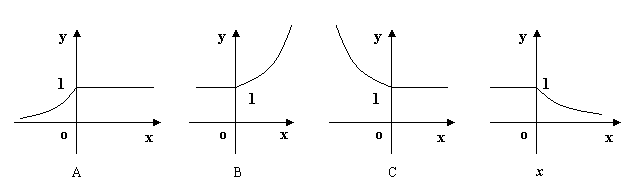
2![]() 的图象是( ).
的图象是( ).
7、已知函数![]() 在区间
在区间![]() 上是减函数,那么b+c ( )
上是减函数,那么b+c ( )
A、有最大值![]() B、有最大值
B、有最大值![]() C、有最小值
C、有最小值![]() D、有最小值
D、有最小值![]()
8.已知函数①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中对于
.其中对于![]() 定义域内的任意一个自变量
定义域内的任意一个自变量![]() 都存在唯一个自变量
都存在唯一个自变量![]() =3成立的函数是( ).
=3成立的函数是( ).
A.③ B.④ C.②③ D.①②④
二、填空题:本大题共7小题,其中13~15题是选做题,考生只能选做两题,三题全答的,只计算前两题得分.每小题5分,满分30分.
9、![]() 是虚数单位,则
是虚数单位,则![]() .
.
10.已知向量![]()
![]() 的夹角的大小为
.
的夹角的大小为
.
11.抛物线![]() 上一点
上一点![]() 到焦点的距离为3,则点
到焦点的距离为3,则点![]() 的横坐标
的横坐标![]() .
.
12.已知 的展开式中的常数项为
的展开式中的常数项为![]() ,
,![]() 是以
是以![]() 为周期的偶函数,且当
为周期的偶函数,且当![]() 时,
时,![]() ,若在区间
,若在区间![]() 内,函数
内,函数![]() 有4个零点,则实数
有4个零点,则实数![]() 的取值范围是 .
的取值范围是 .
13.(坐标系与参数方程选做题)在极坐标系中,点![]() 到直线
到直线![]() 的距离为
.
的距离为
.
14.(不等式选讲选做题)不等式![]() 的解集是
.
的解集是
.
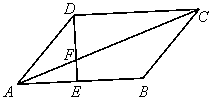 15、(几何证明选讲选做题)如图,平行四边形
15、(几何证明选讲选做题)如图,平行四边形![]() 中,
中,
![]() ,若
,若![]() 的面积等于1cm
的面积等于1cm![]() ,
,
则![]() 的面积等于
cm
的面积等于
cm![]() .
.
三.解答题:本大题共6小题,满分80分.解答须写出文字说明.证明过程和演算步骤.
16、设函数![]() .
.
(Ⅰ)求函数![]() 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(Ⅱ)当![]() 时,
时,![]() 的最大值为2,求
的最大值为2,求![]() 的值,并求出
的值,并求出![]() 的对称轴方程.
的对称轴方程.
17、已知△ABC中,![]()
(1)求角A的大小;
(2)若BC=3,求△ABC周长的取值范围.
18、已知射手甲射击一次,击中目标的概率是![]() .
.
(1)求甲射击5次,恰有3次击中目标的概率;
(2)假设甲连续2次未击中目标,则中止其射击,求甲恰好射击5次后,被中止射击的概率.
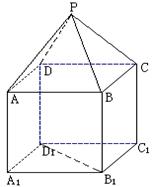 19、如图,P—ABCD是正四棱锥,
19、如图,P—ABCD是正四棱锥,![]() 是正方体,
是正方体,
其中![]()
![]()
(1)求证:![]() ;
;
(2)求平面PAD与平面![]() 所成的锐二面角
所成的锐二面角![]() 的余弦值;
的余弦值;
(3)求![]() 到平面PAD的距离
到平面PAD的距离![]()
20、设函数![]() .
.
(1)求函数![]() 的单调递增区间;
的单调递增区间;
(2)若关于![]() 的方程
的方程![]() 在区间
在区间![]() 内恰有两个相异的实根,求实数
内恰有两个相异的实根,求实数![]() 的取值范围.
的取值范围.
21、已知数列{an}的前n项为和Sn,点![]() 在直线
在直线![]() 上.
上.
数列{bn}满足![]() ,前9项和为153.
,前9项和为153.
(Ⅰ)求数列{an}、{bn}的通项公式;
(Ⅱ)设![]() ,数列{cn}的前n和为Tn,求使不等式
,数列{cn}的前n和为Tn,求使不等式![]() 对一切
对一切![]() 都成立的最大正整数k的值.
都成立的最大正整数k的值.
(Ⅲ)设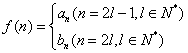 ,问是否存在
,问是否存在![]() ,使得
,使得![]() 成立?若存在,求出m的值;若不存在,请说明理由.
成立?若存在,求出m的值;若不存在,请说明理由.
广州市第41中学2008届高三第二次模拟 理科答卷
班级 姓名 学号 成绩
一、
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
二、满分30分
9、 10、 11、
12、 13、 14、 15、
| 16、 |
| 17、 |
| 18、 |
| 19、
|
| 20、 |
| 21、 |
答案
一、ADCCDABA
二、-8i
90![]() 2 (0,
2 (0,![]()
![]()
![]() 3
3
16、解:(1)![]()
… 2分
则![]() 的最小正周期
的最小正周期![]() , …………4分
, …………4分
且当![]() 时
时![]() 单调递增.
单调递增.
即![]() 为
为![]() 的单调递增区间(写成开区间不扣分).………………6分
的单调递增区间(写成开区间不扣分).………………6分
(2)当![]() 时
时![]() ,当
,当![]() ,即
,即![]() 时
时![]() .
.
所以![]() . ………9分
. ………9分
![]() 为
为![]() 的对称轴.……12分
的对称轴.……12分
17. 解(1)角A=π/3 …………6分
(2)6<周长≤9 …………12分
18、解:(1)设“甲射击5次,恰有3次击中目标”为事件A,则
![]() .
.
答:甲射击5次,恰有3次击中目标的概率为![]() .………………………………6分
.………………………………6分
(2)方法1:设“甲恰好射击5次后,被中止射击”为事件C,由于甲恰好射击5次后被中止射击,所以必然是最后两次未击中目标,第三次击中目标,第一次与第二次至少有一次击中目标,则
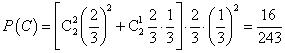 .
.
答:甲恰好射击5次后,被中止射击的概率为![]() .……………………………12分
.……………………………12分
方法2:设“甲恰好射击5次后,被中止射击”为事件C,由于甲恰好射击5次后被中止射击,所以必然是最后两次未击中目标,第三次击中目标,第一次与第二次至少有一次击中目标,则
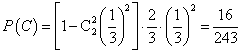 .
.
答:甲恰好射击5次后,被中止射击的概率为![]() .……………………………12分
.……………………………12分
19、解法一:以![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴建立空间直角坐标系…………1分
轴建立空间直角坐标系…………1分
(1)设E是BD的中点,![]() P—ABCD是正四棱锥,∴
P—ABCD是正四棱锥,∴![]() …………2分
…………2分
又![]() , ∴
, ∴![]() ∴
∴![]() ……………………………3分
……………………………3分
∴ ![]() …∴
…∴ ![]() 即
即![]() ……5分
……5分
(2)设平面PAD的法向量是![]() ,
,![]() ………7分
………7分
∴ ![]() 取
取![]() 得
得![]() ,………………8分
,………………8分
又平面![]() 的法向量是
的法向量是![]() …………………9分
…………………9分
∴ 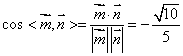 ∴
∴![]() …………………10分
…………………10分
(3)![]() …11分∴
…11分∴![]() 到平面PAD的距离
到平面PAD的距离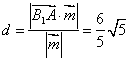 ………14分
………14分
20、解:(1)函数![]() 的定义域为
的定义域为![]() ,……………………………1分
,……………………………1分
∵![]() ,………………………2分
,………………………2分
∵![]() ,则使
,则使![]() 的
的![]() 的取值范围为
的取值范围为![]() ,
,
故函数![]() 的单调递增区间为
的单调递增区间为![]() . ………………………4分
. ………………………4分
(2)方法1:∵![]() ,
,
∴![]() .………………6分
.………………6分
令![]() ,
,
∵![]() ,且
,且![]() ,
,
由![]() .
.
∴![]() 在区间
在区间![]() 内单调递减,在区间
内单调递减,在区间![]() 内单调递增,……………………9分
内单调递增,……………………9分
故![]() 在区间
在区间![]() 内恰有两个相异实根
内恰有两个相异实根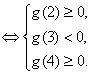 ……12分
……12分
即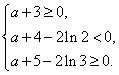 解得:
解得:![]() .
.
综上所述,![]() 的取值范围是
的取值范围是![]() .………………………………14分
.………………………………14分
21、20、解:(Ⅰ)由题意,得![]()
故当![]() 时,
时,![]()
当n = 1时,![]() ,而当n =
1时,n + 5 = 6,
,而当n =
1时,n + 5 = 6,
所以,![]() …………………………………………………… 2分
…………………………………………………… 2分
又![]() ,
,
所以{bn}为等差数列,于是![]()
而![]()
因此,![]() ………………4分
………………4分
(Ⅱ)![]()
![]() …………………………6分
…………………………6分
所以,![]()
![]() …………………………………………7分
…………………………………………7分
由于![]() ,
,
因此Tn单调递增,故![]() ………………………………………………8分
………………………………………………8分
令![]() …………………………………………9分
…………………………………………9分
(Ⅲ)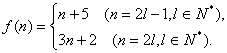
①当m为奇数时,m + 15为偶数.
此时![]() ,
,
所以![]() ………………………………………………11分
………………………………………………11分
②当m为偶数时,m + 15为奇数.
此时![]() ,
,
所以![]() (舍去). ……………………………………13分
(舍去). ……………………………………13分
综上,存在唯一正整数m =11,使得![]() 成立. …………14分
成立. …………14分