2．2．3　向量的数乘

班级　　　　姓名　　　　学号　　　　 年级　　　　学科　　　  

一、概念回顾（认真阅读课本第63,64,65页，回答下面问题）

1．设实数与量的积记为　　　　，它仍表示向量，它的长度是　　　　　　　　；它的方向是　　　　　　　　　　　　　　　　　　　　　　　　　　　　．

2．根据向量数乘的定义，可以证明向量数乘有如下运算律：

（1）　　　　　　　　　　；（2）　　　　　　　　　　；（3）　　　　　　　　　　．

3．向量数乘与实数乘法有哪些相同点和不同点：

相同点　　　　　　　　　　　　　　　　　　　　　　　　　　　　；

不同点　　　　　　　　　　　　　　　　　　　　　　　　　　　　．

二、理解与应用

1．已知，则下列命题正确的是　　　　　　　　　　　　　　　  （　　）

A．　　　　　　B．　　　　　　

C．　　　　　D．

2．已知E、F分别为四边形ABCD的边CD、BC边上的中点，设，，则=　　　　　　　　　　　　　　　　　　　　　　　　　　　　  （　  ）

A．　　　　B．　　 C．　　 D．

3．若化简　　　　　　　　　  （　 ）

A．　　　　　　　　B． 　　　　　 　　C．　　　　　　　　D． 以上都不对

4．已知四边形ABCD是菱形，点P在对角线AC上（不包括端点A、C），则=

（　）　

A．　　　 　　 B．

C． 　　　　　　D．

5．已知、是实数，、是向量，对于命题：

①　　 　　　　②

③若，则　　　　　　　④若，则

其中正确命题为_____________________．

6．计算：

（1）=__________；

（2）=__________．

7．已知向量，，且，则=__________．

8．若向量、满足，、为已知向量，则

=__________； =___________．

9．已知，是两个不共线的向量，，．若与是共线向量，求实数的值．

10．证明：如果存在不全为0的实数，使，那么与是共线向量；如果与不共线，且，那么．

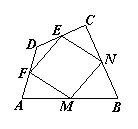
11． 如图，已知：在四边形ABCD中，M、N、E、F分别是边AB、BC、CD、DA的中点．求证：四边形MNEF是平行四边形．

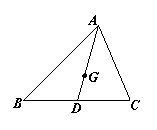
12．如图，在ABC中，G是ABC的重心，证明：

三、方法小结：