高一年级第一学期期末考试数学试卷

（90分钟完成，满分100分）

题号	1－12	13－16	17	18	19	20	21	总分
得分

一、填空题（每小题3分，共36分）本大题共有12小题，只要求直接填写结果，每个

空格填对得3分，否则一律得零分.

1. 命题“如果，那么”的逆命题是　　　　　　　　　.

2. 已知集合，，那么用列举法表示　　　.

3. 不等式的解集是　　　　　　　　　.

4. 全集，，则　　　　　　　　　.

5. 函数的定义域为　　　　　　　　　.

6. 已知函数，则　　　　　　　　　.

7. 若为偶函数，则　　　　　　　　　.

8. 方程在区间内的近似解（精确到）为　　　　　　　　　.

9. 已知函数，且，则与的大小关系是　　　　　　.

10.设函数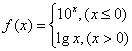，则　　　　　　　　　.

11.把下列不完整的命题补充完整，并使之成为真命题.

若函数的图像与的图像关于　　　　　　　　对称，则函数

　　　　　　　　  　.（填上你认为可以成为真命题的一种情形即可，不必考

虑所有可能的情形）.

12.关于函数，且，有下列命题：

（1）函数的图像关于轴对称；

（2）当时，为增函数；当，函数为减函数；

（3）没有最小值，也没有最大值；

（4）当或时，为增函数.

其中正确命题的序号是　　　　　　　　　.

二、选择题（本大题满分12分）本大题共有4题，每题都给出代号为A、B、C、D四个

结论，其中有且只有一个结论是正确的，必须把正确结论的代号写在题后的圆括号

内，选对得3分，不选、选错或者选出的代号超过一个（不论是否都写在圆括号内），

一律得零分.

13.给出下列函数：

（1）；（2）；（3）；（4）.

其中为奇函数的是(　 )

（A）（1）与（2）　　 （B）（2）与（3）　　　 （C）（3）与（4）　　　 （D）（1）与（3）

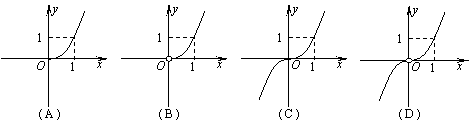
14.已知函数，，则函数的图像是(　 )

15.若不等式成立的充分非必要条件是，则的取值范围是(　 )

（A）（B）（C）（D）

16.一次数学实验中，同学们用图形计算器采集到如下一组数据：

则、的函数关系与下列函数（其中、为待定系数）最接近的是(　 )

（A）（B）（C）（D）

三、解答题（本大题满分52分）本大题共有5题，解答下列各题请写出必要的过程与步

骤.

17.（本大题满分10分）

已知，，且，求实数的取值范围.

18.（本大题满分10分）

判断函数在区间上的单调性，并利用单调性的定义证明你的论.

19.（本大题满分10分）本题共有2个小题，每小题满分5分.

已知函数，.

（1）当时，求函数的最大值与最小值；

（2）求实数的取值范围，使函数在区间上是单调函数.

20.（本大题满分10分）

已知函数且的图像过点，其反函数的图像过点

.求不等式的解集.

21.（本大题满分12分）本题共有2个小题，每小题满分6分.

某大学生响应上海市委号召，拟在2007年自主创业办企业，并举行相应的产品促销活动.经调查测算，该产品的年销售量（即该企业的年产量）万件与年促销费用万

元满足（为常数），如果不搞促销活动，则该产品的年销售量只

能是万件.已知2007年生产该产品的固定投入为万元，每生产万件需要再投入万

元，厂家将每件产品的销售价格定为每件产品年平均成本的倍（企业产品成本包括

固定成本和再投入两部分资金）.

(1)将2007年该产品的利润万元表示为年促销费用万元的函数；

(2)该大学生在2007年的促销活动中投入多少万元时，可使企业的利润最大？并求出最

大利润.

高一年级期末考试数学试卷（简答）

一、填空题

1.如果，那么；2.；3.；4.；5.；6.；

7.；8. ；9.；10.；11.（答案不唯一）；12..

二、选择题13－16.　DBCB.

三、解答.题：

17.的取值范围是.

18.在上是增函数（证明过程略）.

19.（1）；（2），或.

20.；不等式的解集是.

21.（1）；

（2）万元.