高一数学(2008级)第一学期期末试卷
一、选择题:(本大题共12个小题,每小题5分,共60分)
1、已知集合![]() ,
,![]() ,则
,则![]() =( )
=( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D) ![]()
2、已知映射![]() ,集合
,集合![]() 中元素
中元素![]() 在对应法则
在对应法则![]() 下的象是
下的象是![]() ,则121的原象是( )
,则121的原象是( )
(A)8 (B)7 (C)6 (D)5
3、如果函数![]() 在区间
在区间![]() 上是增函数,则实数
上是增函数,则实数![]() 的取值范围是( )
的取值范围是( )
(A)![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D)
![]()
4、函数![]() 的反函数是( )
的反函数是( )
(A)![]() (B)
(B)
![]()
(C) ![]() (D)
(D)
![]()
5、设![]() 是简单命题,则
是简单命题,则![]() 为真,是
为真,是![]() 为真的( )
为真的( )
(A) 充分不必要条件 (B)必要不充分条件
(C) 充要条件 (D) 既不充分也不必要条件
6、给出函数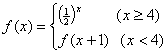 ,则
,则![]() 等于( )
等于( )
(A)![]() (B)
(B) ![]() (C)
(C)
![]() (D)
(D)
![]()
7、已知:![]() ,
,![]() ,
,![]() ,则( )
,则( )
(A)![]() 是
是![]() 的等比中项
的等比中项
(B) ![]() 是
是![]() 的等差中项
的等差中项
(C) ![]() 既是
既是![]() 的等差中项,又是
的等差中项,又是![]() 的等比中项
的等比中项
(D) ![]() 既不是
既不是![]() 的等差中项,又不是
的等差中项,又不是![]() 的等比中项
的等比中项
8、已知数列![]() 的通项公式
的通项公式![]() ,其前
,其前![]() 项和
项和![]() 达到最大值时
达到最大值时![]() 的值是( )
的值是( )
(A)26 (B)25 (C)24 (D)23
9、某种商品提价25%,现在恢复成原价,则应降价( )
(A) 25% (B) 15% (C) 10% (D) 20%
10、等差数列![]() 的前
的前![]() 项和为
项和为![]() ,若已知
,若已知![]() 的值,则一定可求( )
的值,则一定可求( )
(A) ![]() (B)
(B)
![]() (C)
(C)
![]() (D)
(D)
![]()
11、函数![]() 的单调递增区间是( )
的单调递增区间是( )
(A)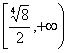 (B)
(B)![]() (C)
(C) 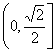 (D)
(D)
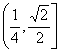
12、设函数![]() ,满足
,满足![]() ,则
,则![]() 与
与![]() 的大小关系是( )
的大小关系是( )
(A) ![]() (B)
(B)
![]()
(C) ![]() (D)
(D)
![]()
二、填空题:(本大题共4个小题,每小题4分,共16分)
13、函数![]() ,若它的反函数是
,若它的反函数是![]() ,则
,则![]() =
。
=
。
14、设函数![]() 的图象与
的图象与![]() 的图象关于直线
的图象关于直线![]() 对称,则函数
对称,则函数![]() 的递增区间为
。
的递增区间为
。
15、设![]() 是等差数列
是等差数列![]() 的前
的前![]() 项和,已知
项和,已知![]() ,
,![]() ,若
,若![]() ,则
,则
![]() = 。
= 。
16、定义在![]() 上的函数
上的函数![]() 满足
满足![]() ,则
,则![]()
![]() =
。
=
。
三、解答题:(共74分)
17、(本小题12分)已知集合![]() ,
,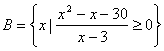 ,且
,且![]() ,试求实数
,试求实数![]() 的取值范围。
的取值范围。
18、(本小题12分)已知![]() ,(1)求
,(1)求![]() 的解析式;(2)求
的解析式;(2)求![]() 的值。
的值。
19、(本小题12分)已知函数![]() 的图象恒过定点
的图象恒过定点![]() ,且点
,且点![]() 又在函数
又在函数![]() 的图象上。(1)求函数
的图象上。(1)求函数![]() 的反函数;(2)若
的反函数;(2)若![]()
![]()
![]() 成等差数列,求
成等差数列,求![]() 的值。
的值。
20、(本小题12分)在占地3250亩的荒山上建造森林公园,2000年春季开始植树100亩,以后每年春季都比上一年多植树50亩,直到荒山全部绿化完为止。(1)哪一年春季才能将荒山全部绿化完?(2)如果新植的树每亩木材量是2m3,树木每年自然增长率是20%,那么全部绿化完,该森林公园的木材蓄量是多少m3?
21、(本小题12分)已知数列![]() 的首项
的首项![]() ,其前
,其前![]() 项的和为
项的和为![]() ,且对于任意的正整数
,且对于任意的正整数![]() ,有
,有![]() 成等差数列。(1)求证:数列
成等差数列。(1)求证:数列![]() 成等比数列;(2)求数列
成等比数列;(2)求数列![]() 的通项公式。
的通项公式。
22、(本小题14分)已知函数![]() (1)求
(1)求![]() 的定义域和值域;(2)讨论函数
的定义域和值域;(2)讨论函数![]() 的单调性并用单调性的定义证明。(3)设
的单调性并用单调性的定义证明。(3)设![]() ,解关于
,解关于![]() 的不等式
的不等式![]() 。
。
参考答案
一、1.A ;2.B;3.B;4.A;5.B;6.C;7.B;8.C;9.D;10.B;11.A;12.C
二、13.1;14.![]() ;15.18;16.7.
;15.18;16.7.
三、17.![]()
18.(1)![]() ;(2)
;(2)![]()
19.(1)![]() ;(2)
;(2)![]()
20.(1)2009年春季才能绿化完全部荒山;(2)13172m3
21.(1)略;(2)![]()
22.(1)定义域为![]() ,值域为
,值域为![]() ;(2)当
;(2)当![]() 时,
时,![]() 为定义域内的增函数,当
为定义域内的增函数,当![]() 时,
时,![]() 为定义域内的减函数,证明(略);(3)
为定义域内的减函数,证明(略);(3)![]()