高一数学第一学期期终考试
一．选择题（每小题3分）
1．设集合M=
，N=
，则
（ ）
A． B．
C．
D．
2．
是
的
（ ）
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分又不必要条件
3．已知
，
是第四象限角，则
（ ）
A．
B．－ C．
D．
4．等比数列前7项和为48，前14项和为60，则前21项和为 （ ）
A．180 B．108 C．75 D．63
5．若函数
的反函数恒过P点，则P为
（ ）
A．（1，3） B．（4，1） C．（1，4） D．（3，1）
6．已知等差数列
中，
，公差
，则使前
项和
取得最大值时的自然数为
（ ）
A．4和5 B．5和6 C．6和7 D．不存在
7．已知
，
，则
（ ）
A．25 B．50 C．100 D．150
８．函数
，（
）的图象关于 （ ）
Ａ．
轴对称 Ｂ．
轴对称 Ｃ．原点对称 Ｄ．
对称
９．一个等差数列的项数为２项，若
，
，且
，则该数列的公差为 （ ）
Ａ．３ Ｂ．－３ Ｃ．－２ Ｄ．－１
10．满足
（ ）
Ａ．
Ｂ．
Ｃ．
Ｄ．
11．甲向银行一次性贷款Ａ万元，每年等额还款，１０年后还清。设银行贷款利息按年息
的复利计算，则甲每年应还贷款 （ ）
Ａ．
Ｂ．
Ｃ．
Ｄ．
12．已知函数
是R上的增函数，A（0，-1）、B（3，1）是其图象上的两点，则
的解集是 （ ）
A、
B、
C、
D、
二．填空题
13．⑴
的单调递减区间 ；
⑵
的图象与
的图象关于对称，则函数
的单调递增区间 。
14．已知数列中，
，又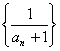
是等比数列，则
＝ 。
15．
的定义域为
，则的定义域 。
16．
，则⑴
＝ ；⑵
＝ 。
17．等比数列的前项和
，则
。
18．设等差数列，
的前项和为
且
，则
。
舟山中学2005学年第一学期高一普通班班期终考试
数学答卷
一．选择题（共３６分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
一．填空题 （每空２分，共１６分）
13． ⑴ ⑵ 。14． 。15． 。16． ⑴ ⑵ 。17． 。18． 。
三． 解答题（共６大题．共４８分）
19．⑴求值：
；
⑵求
的值域。
20．⑴求
⑵
,若在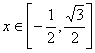
上是单调函数，求
的取值范围。
21．已知等差数列，
, 
且公差d > 0
⑴求的通项公式；⑵ 令
，求数列的前项和。
22．已知数列的首项
，其前项和为，且对任意正整数，有
成等差，⑴求证：
成等比数列；⑵求的通项公式。
23．据记载，某地区在1990至1993年间，沙漠面积不断扩大，数据如下（面积：万公顷）：
| 年份 | 沙漠面积 | 比上一年增加的沙漠面积 |
| 1990年年底 |
| |
| 1991年年底 | 80.2 | 0.2 |
| 1992年年底 | 80.5 | |
| 1993年年底 | 80.9 |
80.0⑴请填写表格中未完成的部分,并观察沙漠面积每年比上一年增加量的规律,如果以后每年的沙漠面积仍按此规律扩大,那么到2010年年底,该地区的沙漠面积将会达到多少万公顷?
⑵该地区自1994年年初起开始在沙漠上植树造林,使沙漠变绿洲.已知第一年植树1万公顷,以后每一年植树面积比上一年增加1%,同时从1994年起沙漠扩展的面积每年都控制在0.1万公顷,那么到2010年年底,该地区的沙漠面积还剩多少万公顷?(结果精确到0.1万公顷)
以下数据仅供参考:
,
, 
, 
,
24．函数定义在Ｒ上，对任意
都有
,
且当
。 ⑴已知
求
的值；
⑵求证：
；⑶证明在Ｒ上单调递减；
⑷设
，
，若
，试确定
的取值范围。
附加题(6分)
已知数列中，
且
其中
。
求的通项公式。