高一数学阶段测试一
一、 选择题(本大题共12小题,每小题3分,共36分,在每小题给出的四个选项中,只有一个是符合题目要求的)
1.集合A={ x x = y, y∈R},B={yy=x2, x∈R}则A∩B=:
A. {0 , 1}
B. {(0 , 1)} C. {yy≥0} D. ![]()
2.已知直线![]() 和平面
和平面![]() ,下列推论中错误的是:
,下列推论中错误的是:
A. ![]() B.
B.![]()
C. ![]() D.
D.![]()
3. 若直线![]() 和2x+3y+1=0互相平行,则
和2x+3y+1=0互相平行,则![]() =:
=:
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.有一棱长为![]() 的正方体框架,其内放置一气球,是其充气且尽可能地膨胀(仍保持为球的形状),则气球表面积的最大值为:
的正方体框架,其内放置一气球,是其充气且尽可能地膨胀(仍保持为球的形状),则气球表面积的最大值为:
A.![]() B.2
B.2![]() C.3
C.3![]() D.4
D.4![]()
5.要得到函数![]() 的图象,只需将函数
的图象,只需将函数![]() 的图象:
的图象:
A.向左平移1个单位 B.向右平移1个单位
C.向上平移1个单位 D.向下平移1个单位
6. 已知点P(3,2)与点Q(1,4)关于直线l对称,则直线l的方程为:
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.函数![]()
![]() 的定义域为:
的定义域为:
A.(![]() ,+∞) B.[1,+∞
,+∞) B.[1,+∞![]() C.(
C.(
![]() ,1
,1![]() D.(-∞,1)
D.(-∞,1)
8.过点A(1,3)作直线![]() ,若
,若![]() 经过点(a,0)和(0,b)且a,b∈N*,则可作出的不同直线
经过点(a,0)和(0,b)且a,b∈N*,则可作出的不同直线![]() 的条数为:
的条数为:
A.1 B.2 C.3 D.多于3
9.P为矩形ABCD所在平面外一点,且PA⊥平面ABCD,P到B,C,D三点的距离分别
是![]() ,
,![]() ,
,![]() ,则P到A点的距离是:
,则P到A点的距离是:
A.1 B.2
C.![]() D.4
D.4
10. 方程![]() 根的情况是:
根的情况是:
A.有两个正根 B.一个正根一个负根
C.有两个负根 D.仅有一个实数根
11.设△ABC的一个顶点是A(3,-1),∠B,∠C的平分线方程分别是![]() ,则直线BC的方程是
,则直线BC的方程是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.
设函数![]() ,区间M=[
,区间M=[![]() ,b](
,b](![]() <b),集合N={
<b),集合N={![]() },则使M=N成立的实数对(
},则使M=N成立的实数对(![]() ,b)有:
,b)有:
A.0个 B.1个 C.2个 D.无数多个
二、 (本大题共6小题,共18分,把答案填在题中横线上)
13.若长方体三个面的面积分别是![]() ,则长方体的体积为
.
,则长方体的体积为
.
14.函数y=![]() 的值域为_________________.
的值域为_________________.
15.平行四边形的两条对角线交点为![]() ,一条边所在的直线方程为
,一条边所在的直线方程为![]() ,则该边的对边所在的直线方程是
,则该边的对边所在的直线方程是
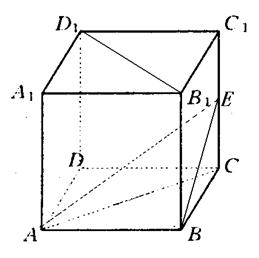
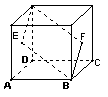
16.如图,E、F分别为正方体的面![]() ,面
,面![]() 的中心,则四边形
的中心,则四边形![]() 在该正方体的面上的射影可能是
(填出所有可能的序号)
在该正方体的面上的射影可能是
(填出所有可能的序号)
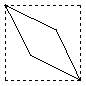
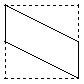
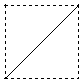
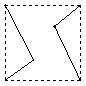
① ② ③ ④
17. 已知实数x,y满足![]() 的最小值为
.
的最小值为
.
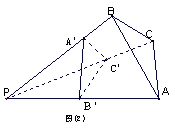
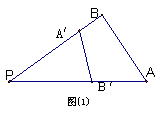
18. 由图(1)有面积关系: ![]() 则由(2) 有体积关系:
则由(2) 有体积关系: ![]()
答题卷
姓名 班级 得分
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
|
|
二、填空题
13. 14. 15.
16. 17. 18.
三、解答题:本大题共小题,共46分,解答应写出文字说明、证明过程或演算步骤.
19.设集合![]() ,集合
,集合![]() .
.
(Ⅰ)设P![]() Q,求实数
Q,求实数![]() 的取值范围。
的取值范围。
(Ⅱ)若P∩Q=![]() ,求实数
,求实数![]() 的值. (本题8分)
的值. (本题8分)
20.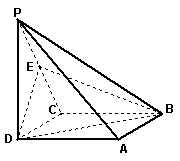 在四棱锥
在四棱锥![]() 中,底面
中,底面![]() 是正方形,侧棱
是正方形,侧棱![]() ,
,![]() ,E是
,E是![]() 的中点。
的中点。
(Ⅰ)证明:![]()
(Ⅱ)求![]() 与底面所成的角的正切值. (本题8分)
与底面所成的角的正切值. (本题8分)
21. △ABC的顶点为A(1,1),B(4,1),C(1,5).
(Ⅰ)求边BC上的高所在直线l的方程;
(Ⅱ)已知直线m过点A,且与B,C两点距离相等,求直线m的方程;(本题8分)
22. 设![]() (
(![]() 是自然对数的底,
是自然对数的底,![]() )是奇函数.
)是奇函数.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)判断![]() 在定义域上的奇偶性,并证明你的结论. (本题10分)
在定义域上的奇偶性,并证明你的结论. (本题10分)
23.
在正方体![]() 中,棱长
中,棱长![]() . E为棱
. E为棱![]() 的中点
的中点
(Ⅰ)求证:![]() ;
;
(Ⅱ)求二面角C-AE-B的平面角的正切值;
(III)求点![]() 到平面EAB的距离。(本题12分)
到平面EAB的距离。(本题12分)