高一数学期末试卷
一、填空题（每小题4分，共48分）：
1、 若集合
，则
____
_________；
2、 函数
的定义域为__
_______;
3、若
,则实数
的取值范围是__
____________；
4、函数
，则它的反函数
_
______；
5、化简：
=____
____；
6、若
，则函数
的最大值为______
_______；
7、已知二次函数
满足
，且在
是减函数，
则
的大小关系为__
_________；
8、“
”是“
”成立的__必要不充分__条件（填写“充分不必要、必要不充分、
充要或既不充分也不必要”） 。
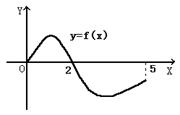
9、设奇函数的定义域为
。若当
时, 的
图象如右图,则不等式
的解是 
10、若函数
对其定义域内的任意两个值
，满足
，则的一个可能的解析式为
_
__等_______________（写出一个即可）。
11、设函数的定义域为R，有下列三个命题：（1）若存在常数M，使得对任意x∈R，有f(x)≤
M，则M是函数f(x)的最大值；(2)若存在x0∈R，使得对任意x∈R，且x≠x0，有f(x)＜f(x0)，
则f(x0)是函数f(x)的最大值；(3)若存在x0∈R，使得对任意x∈R，有f(x)≤f(x0)，则f(x0)
是函数f(x)的最大值。这些命题中，真命题的个数是___2_____个。
12、若函数若函数
在
上为增函数,则实数的取值范围是 
.
二、选择题（每小题3分，共12分）：
13、已知a、b、c满足
，且
，那么下列选项中不一定成立的是 （ C ）
（A）
（B）
（C）
（D）
14、已知是定义在R上的偶函数，并且满足
，当
时，
，
则
=（ D ）
（A）
（B）
（C）
（D）
15、下列函数中：①
；② 
；③
④
⑤
，奇函数的个数为（ B ）个。
（A） 1 （B）2 （C）3 （D）4
16、已知农民收入由工资性收入和其他收入两部分构成。2004年某地区农民人均收入为3150
元（其中工资性收入为1800元，其他收入为1350元），预计该地区自2005年起的5年内，
农民的工资性收入将以6%的年增长率增长，其他收入每年增加160元。根据以上数据，2009
年该地区农民人均收入介于（ B ）
（A）4200~4400 （B）4400~4600 （C）4600~4800 （D）4800~5000
三、解答题：（共40分）
17、（7分）已知集合
，若
，求
18、（7分）已知二次函数
的最大值为3，求实数的值。
19、（8分）已知
且
，关于
的不等式
的解集是
，解关于的不等式：
20（8分）奇函数是R上的减函数，对任意实数恒有
成立，求实数的取值范围。
21、（10分）某村计划建造一个室内面积为800平方米的矩形蔬菜温室。在温室内，沿左、右两侧与后侧内墙各保留1米宽的通道，沿前侧内墙保留3米宽的空地。设矩形温室的左侧边长为米，蔬菜的种植面积为
平方米。（1）写出关于的函数关系式，并写出定义域；（2）求矩形蔬菜温室的最大种植面积，并求出此时的值。
解：设矩形温室的左侧边长为a m，后侧边长为b m，则 ab=800.
蔬菜的种植面积 
所以 
当
答：当矩形温室的左侧边长为40m，后侧边长为20m时，蔬菜的种植面积最大，最大种植面积为648m2.