2005-2006高中数学必修1第三章直线方程测试题

　 考试时间：100分钟　　总分：150分　出题人：肖海涛

一选择题（共55分，每题5分）

1. 已知直线经过点A(0,4)和点B（1，2），则直线AB的斜率为（　 ）

A.3　　　　 B.-2　　　　  C. 2　　　　 D. 不存在

2．过点且平行于直线的直线方程为（　）

A．　 B．　　C．　　D．

3. 在同一直角坐标系中，表示直线与正确的是（　 　）

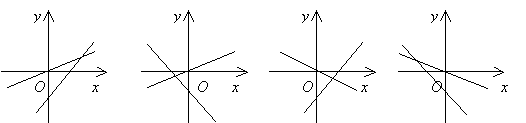
　 A　　　　　　　　　　 B　　　　　　 C　　　　　　　 D

4．若直线x+ay+2=0和2x+3y+1=0互相垂直，则a=（　　）

A．　　　　B．　　　 　　 C．　　　　D．

5.过(x₁，y₁)和(x₂，y₂)两点的直线的方程是(　　)

L3

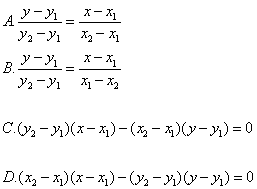
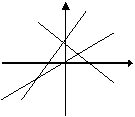6、若图中的直线L₁、L₂、L₃的斜率分别为K₁、K₂、K₃则（　　 ）

L2

　　　　  A、K₁﹤K₂﹤K₃

B、K₂﹤K₁﹤K₃

o

x

　　　　  C、K₃﹤K₂﹤K₁

L1

　　　　  D、K₁﹤K₃﹤K₂

　　　　　　　　　　

7、直线2x+3y-5=0关于直线y=x对称的直线方程为（　 ）

A、3x+2y-5=0　　　　　　　　　 B、2x-3y-5=0

C、3x+2y+5=0　　　　　　　　　 D、3x-2y-5=0

8、与直线2x+3y-6=0关于点(1,-1)对称的直线是（　　 ）

A.3x-2y-6=0　　　　　　　　　 　B.2x+3y+7=0　

C. 3x-2y-12=0　　　　　　　　　  D. 2x+3y+8=0

9、直线5x-2y-10=0在x轴上的截距为a,在y轴上的截距为b,则（　　）

A.a=2,b=5;　　 B.a=2,b=;　　　C.a=,b=5;　　 D.a=,b=.

10、直线2x-y=7与直线3x+2y-7=0的交点是（　　）

A  (3,-1)　B　(-1,3)　C  (-3,-1)　D　(3,1)

11、过点P(4,-1)且与直线3x-4y+6=0垂直的直线方程是（　　）

A  4x+3y-13=0　　  B　 4x-3y-19=0

C  3x-4y-16=0　　  D　 3x+4y-8=0

二填空题（共20分，每题5分）

12. 过点（1，2）且在两坐标轴上的截距相等的直线的方程　　　　　　　　　　　 _ __________；

13两直线2x+3y－k=0和x－ky+12=0的交点在y轴上，则k的值是　　　　　

14、两平行直线的距离是　　　　　　　　　  。

15空间两点M1（-1,0,3）,M2(0,4,-1)间的距离是　　　　　　　　　　

 

三计算题（共71分）

16、（15分）已知三角形ABC的顶点坐标为A（-1，5）、B（-2，-1）、C（4，3），M是BC边上的中点。（1）求AB边所在的直线方程；（2）求中线AM的长（3）求AB边的高所在直线方程。

17、（12分）求与两坐标轴正向围成面积为2平方单位的三角形，并且两截距之差为3的直线的方程。

18.（12分） 直线与直线没有公共点，求实数m的值。

19．（16分）求经过两条直线和的交点，且分别与直线（1）平行，（2）垂直的直线方程。

20、（16分）过点（２，３）的直线Ｌ被两平行直线Ｌ_１：２ｘ－５ｙ＋９＝０与

Ｌ_２：２ｘ－５ｙ－７＝０所截线段ＡＢ的中点恰在直线ｘ－４ｙ－１＝０上，求直线Ｌ的方程

2005-2006高中数学必修1第三章直线方程测试题答案

1-5　　BACAC　6-10　 AADBA　11　 A　　12.y=2x或x+y-3=0　13.±6　　　　　　 14、　 15.

16、解：（1）由两点式写方程得 ，……………………3分

即　6x-y+11=0……………………………………………………4分

或　 直线AB的斜率为　……………………………1直线AB的方程为　………………………………………3分

　　 即　6x-y+11=0…………………………………………………………………4分

（2）设M的坐标为（），则由中点坐标公式得

　 故M（1，1）………………………6分

…………………………………………8分

(3)因为直线AB的斜率为k_AB=········（3分）设AB边的高所在直线的斜率为k

则有··········（6分）

所以AB边高所在直线方程为········（10分）

17．解：设直线方程为则有题意知有

又有①此时

 ②

18．方法（1）解：由题意知

方法（2）由已知，题设中两直线平行，当

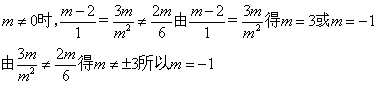
当m=0时两直线方程分别为x+6=0,-2x=0,即x=-6,x=0,两直线也没有公共点，

综合以上知，当m=-1或m=0时两直线没有公共点。

19解：由，得；…………………………………………….….2′

∴与的交点为（1，3）。…………………………………………………….3′

（1）　　  设与直线平行的直线为………………4′

则，∴c＝1。…………………………………………………..6′

∴所求直线方程为。…………………………………………7′

方法2：∵所求直线的斜率，且经过点（1，3），…………………..5′

∴求直线的方程为，……………………….. …………..…6′

即。………………………………………….….. ……………7′

（2）　　  设与直线垂直的直线为………………8′

则，∴c＝－7。…………………………………………….9′

∴所求直线方程为。……………………………………..…10′

方法2：∵所求直线的斜率，且经过点（1，3），………………..8′

∴求直线的方程为，……………………….. ………….9′

即　。………………………………………….….. ……….10′

20、解：设线段ＡＢ的中点P的坐标（a，b），由P到L₁，_、L₂的距离相等，得

经整理得，，又点P在直线ｘ－４ｙ－１＝０上，所以

解方程组　得　即点P的坐标（-3，-1），又直线L过点（２，３）

所以直线Ｌ的方程为，即