![]()
 高一第一学期期终数学测试(三)
高一第一学期期终数学测试(三)
(完卷时间90分钟,满分100分)
| 题 号 | 一 | 二 | 三 | 总 分 |
| 得 分 |
一、填空题(每题3分,共36分)
1.复数3+2i的共轭复数是 。
2.已知集合A={0,1},则集合A的真子集的个数为 个。
3.设A={x x≥ –1},B={xx ≤ 3},用区间表示A∩B= 。
4.已知函数![]() (x>–1),
(x>–1),![]() (x¹0),若
(x¹0),若![]() ,则
,则![]() =
。
=
。
5.函数![]() 的定义域是
。
的定义域是
。
6.实数x>0,则函数y=![]() 的最小值是 。
的最小值是 。
7.函数y=![]() (x≠1)的反函数为
。
(x≠1)的反函数为
。
8.“x>5”是“x>2”的 条件。
9. 若函数y=f(x)为定义在R上的奇函数,则f(0) = 。
10.对数方程lg(x2–4x+9)=lg6的解为 。
11.若指数函数f(x)=![]() 是增函数,则实数a的取值范围是 。
是增函数,则实数a的取值范围是 。
 12.已知
12.已知![]() 是定义域为(–4,4)的奇函数,它在
是定义域为(–4,4)的奇函数,它在![]() ,+∞)的图象如右图所示,则f(x)>0的解集为
。
,+∞)的图象如右图所示,则f(x)>0的解集为
。
二、选择题(每题3分,共12分)
13.![]() 与
与![]() 表示同一函数的是
( )
表示同一函数的是
( )
(A)![]() 与
与![]() (B)
(B)![]() 与
与![]()
(C)![]() 与
与![]() (D)
(D)![]() 与
与![]()
14.下列命题中,假命题是 ( )
(A)若Z为实数,则![]() =Z
(B)若
=Z
(B)若![]() =Z,则Z为实数
=Z,则Z为实数
(C)若Z为实数,则Z.![]() 为实数
(D)若Z.
为实数
(D)若Z.![]() 为实数,则Z为实数
为实数,则Z为实数
15.若函数![]() 为偶函数,则它在区间(–4,0)上是 ( )
为偶函数,则它在区间(–4,0)上是 ( )
(A)增函数 (B)减函数 (C)先增后减 (D)先减后增
16.设集合M={xx=2k+1, k∈Z},N={xx=4n±1, nÎZ},则下列关系正确的是( )
(A)![]() (B)
(B)![]() (C)M=N (D)M、N互不包含.
(C)M=N (D)M、N互不包含.
三、解答题(本大题共52分)
17.(本题6分) 解不等式:![]()
18.(本题8分) 解方程:3z+z=1–3i
 19.(本题9分) 若函数
19.(本题9分) 若函数![]() (x2–1),
(x2–1),
(1)化简函数的解析式,并写出它的定义域;
(2)判断函数f(x)的奇偶性;
(3)写出函数的单调区间,并画出函数的图象。
20.(本题9分) 已知复数![]() ,
,
(1)若![]() ,求
,求![]() ;
;
(2)若![]() (a≤1),
(a≤1),![]() ,求
,求![]() 的取值范围。
的取值范围。
21.(本题10分) 如图四边形ABCD是边长为1的正方形,K是对角线BD上的一点。连接CK,并延长交BA(或其延长线)于M,设DK=x。
(1)用x表示BM;
(2)用x分别表示ΔCKD及ΔKMB的面积;
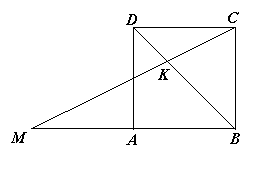 (3)当x取得何值时,ΔCKD及ΔKMB的面积和S最小?此最小值是多少?
(3)当x取得何值时,ΔCKD及ΔKMB的面积和S最小?此最小值是多少?
22.(本题10分) 设![]() ,函数y=2x+3
(
,函数y=2x+3
(![]() )及y=x2 (
)及y=x2 (![]() )的值域分别为集合B、C,且
)的值域分别为集合B、C,且![]() ,求实数a的取值范围。
,求实数a的取值范围。
参考答案
一、填空题
1、3–2i
2、3 3、[–1,3] 4、x,(x>–1且x≠0) 5、![]() 1, 5]
1, 5]
6、4
7、y=![]() (x≠2) 8、充分不必要条件 9、0
(x≠2) 8、充分不必要条件 9、0
10、x=1或x=3 11、a>4 12、(–4,–2)∪(0,2)
二、选择题
13、C 14、D 15、A 16、C
三、解答题
17、由不等式![]() 得:
得: ![]() 1分
1分
即:![]() 2分
2分
所以原不等式的解为:![]() 3分
3分
18、设z=a+bi (a、b∈R), 1分
代入原方程得:3(a+bi)+![]() =1–3i ,
=1–3i ,
即:3a+![]() +3bi = 1–3i
2分
+3bi = 1–3i
2分
所以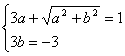 1分
1分
解之得:![]() 或
或 2分
2分
经检验 得z= –i 2分
19、(1) ![]() (x2–1)=
(x2–1)=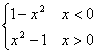 2分
2分
(2)因为f(–x)=……= –f(x),所以f(x)为奇函数 2分
其单调递增区间为(–∞, 0)以及(0, +∞) 2分
正确作出图象 3分
20、(1)因为![]() =
=![]() , 又
, 又![]() =
=![]() ,
,
所以Z1+Z2= –1 3分
(2)因为![]() (a≤1),
(a≤1),
所以Z1=![]()
W=Z1+2=![]() 3分
3分
W=![]() =
=![]() ,0≤a2≤1
,0≤a2≤1
W的取值范围为[1,![]() ]
3分
]
3分
21、(1)在正方形ABCD中,AB∥CD,所以ΔCKD∽ΔMKB,
故有:![]() ,即:
,即:![]() ,
2分
,
2分
所以 BM=![]() ,(0<x<
,(0<x<![]() )
1分
)
1分
(2)SΔCKD=![]() (0<x<
(0<x<![]() );SΔMKB =
);SΔMKB =![]() (0<x<
(0<x<![]() ) 2分
) 2分
(3)S= SΔCKD +SΔMKB =![]() +
+![]() (0<x<
(0<x<![]() )
)
=![]() ≥
≥![]() =
=![]() –1
3分
–1
3分
当且仅当2x=![]() ,即x=1时,S最小=
,即x=1时,S最小=![]() –1
2分
–1
2分
22、因为函数y=2x+3 (![]() )的值域为B=[–1, 2a+3]
1分
)的值域为B=[–1, 2a+3]
1分
当–2≤a<0时,函数y=x2 (![]() )的值域C=[a2,4]
1分
)的值域C=[a2,4]
1分
当0≤a<2时,函数y=x2的值域C=[0,4] 2分
当a≥2时,函数y=x2 (![]() )的值域B=[0,a2]
1分
)的值域B=[0,a2]
1分
若使![]() ,则有:
,则有:
(1)当–2≤a<0时,–1≤a2且4≤2a+3,即a≥![]() ,故aÎF 1分
,故aÎF 1分
(2)当0≤a<2时,–1≤0且4≤2a+3,即a≥![]() ,故
,故![]() ≤a<2
1分
≤a<2
1分
(3)当a≥2时,–1≤0且a2≤2a+3,即–1≤a≤3,故2≤a≤3 1分
综上所述:满足条件![]() 的a的取值范围是
的a的取值范围是![]() ≤a≤3 2分
≤a≤3 2分
(如果仅用数形结合方法,而没有具体说明过程,相应给一半分数)