高一年级数学抽考试卷

（· 文）

时间：120分钟　 总分：160分

一、选择题：（10×5=50）

1．符合条件的集合的个数是--------------------------（　 ）

A．2 ；　　　 B.3　　　  C.4　　　　　 D.5

2．若那么：等于-------------------------------------------------------（　 ）

A．　　　　B.　　　　C.　　  D.

3．命题“若角，则是等边三角形”的否命题是---------------（　 ）

A．假命题；　　　　　　　　　　　  B.与原命题真值相同；

C．与原命题的逆否命题真值相同；　　D.与原命题的逆命题真值相同.

4．“”是“”的-----------------------------（　 ）

A．充分不必要条件；B.必要不充分条件；C.充要条件；D.既不充分也不必要条件.

5．给出以下命题：①；②；其中真命题的个数是 --------------------------------------------------------（　 ）

A．0　　　　　 B.1　　　　　 C.2　　　　　 D.不确定.

6．已知集合，映射，在的作用下像0的原像是-----------------------------------------------------------（　 ）

A．1　　　　　 B.-1　　　　  C.0　　　　　 D.2

7．已知是定义R上的奇函数，当时：，则在R上的表达式------------------------------------------------------------------（　 ）

A．； B.； C.；　 D..

8．若二次函数的递增区间为，则二次函数的递减区间为--------------------------------------------------------------（　 ）

A．；　 B.；　 C.；　　D..

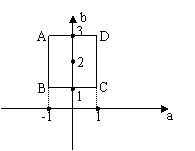9．已知函数在区间上的值域为，那么以为横坐标，为纵坐标的点的轨迹为图中---------------------------------------------（　 ）

　　　　　　　　　　　　　　　　　 A．点

　　　　　　　　 　　　　　　　　　B．线段：AB、CD.

　　　　　　　　　　　　　　　　　 C．线段: AD、BC.

　　　　　　　　　　　　　　　　　 D．线段：AB、AD.

10．已知奇函数的图像是两条直线的一部分（如图所示），其定义域为，则不等式的解集是--------------------------------------（　 ）

A．； B.；

C．； D.

二、填空题：（6×5=30）

11．比较大小：　　　　 .

12．已知则　　　　　　　 .

13．若非空集合，则能使成立的所有的集合是　　　　　　　　　　　　  .

14．函数的单调递增区间是　　　　　　　　　　　　　　　  .

15．已知奇函数偶函数满足：则函数的表达式是　　　　　　　　　　　　　　  .

16．已知则必有　　　　 .（填上序号）

①；②；③；④.

三、解答题：（共80分）

17．(10分) 解指数方程：

18． （12分）设；若，求的取值范围.

19．（14分）已知，求的解析式.

20．（14分）设为常数）.

（1）时，求的最小值；（2）求所有使的值域为的的值.

21．（14分）函数对一切实数均有成立，且.

（1）求的值；（2）当恒成立时，求的取值范围.

22．（16分）已知函数 的图像上有两点，满足

　

（1）　　　 求证：；（2）求证：的图像被轴截得的线段长的取值范围是；

（3）问能否得出中至少有一个数为正数？证明你的结论.