高一上学期数学期中测试卷　　　　　　　　　　　　　　　  第Ⅰ卷  (选择题　共30分)

一、选择题(本大题共10小题，每小题3分，共30分，在每小题给出的四个选项中，只有一项是符合题目要求的)

1.设全集I=R，M={xx≥3},N={x0≤x<5},则_R(M∪N)等于(　　)

A.(－3，0)　　　　　　　　　　　　　　　B.(－3，3)∪(3，5)

C.(－3，5)　　　　　　　　　　　　　　　D.(－3，0)∪(3，5)

【解析】M∪N={xx≤－3或x≥0}

∴_R(M∪N)=(－3,0).

【答案】A

2.已知集合A满足{1,2}A{1,2,3,4,5,6}，则满足题意的集合A一共有(　　)

A.7个　　　　　　　 B.8个　　　　　　　 C.15个　　　　　　　D.16个

【解析】集合A是在集合{1，2}增添从3、4、5、6中取0个、1个、2个、3个数字的元素组成，共有1+4+6+4=15个.

【答案】C

3.关于x的不等式<0 (a+b<0)的解集为(　　)

A.{xx<－a}　　　　　　　　　　　　　　 B.{xx<－a或x>b}

C.{xx<b或x>－a}　　　　　　　　　　　 D.{xb<x<－a}

【解析】<0(x+a)(x－b)>0又b<－ax<b或x>－a.

【答案】C

4.有两个命题：p:四边形的一组对边平行且相等；q:四边形是矩形，则p是q成立的(　　)

A.充分不必要条件　　　　　　　　　　　　B.必要不充分条件

C.充要条件　　　　　　　　　　　　　　　D.既不充分也不必要条件

【解析】一组对边平行且相等的四边形是平行四边形，但不一定是矩形，而矩形一定是平行四边形，∴pq,qp.

【答案】B

5.已知函数g(x)=1－2x,f［g(x)］=,则f()等于(　　)

A.1　　　　　　　　 B.4　　　　　　　　 C.15　　　　　　　　　　D.30

【解析】若g(x)=,则x=

∴f()=f［g()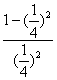］==16－1=15.

【答案】C

6.函数y=的值域为(　　)

A.{yy≠1且y∈R}　　　　　　　　　　　 B.(－1,1)

C.［－1,1］　　　　　　　　　　　　　　 D.［0,1］

【解析】y=

∵e^x+1>1　∴0<<1

∴0<<2　∴－1<1－<1

即－1<y<1

【答案】B

7.设a>0,a≠1，函数y=log_ax的反函数和y=log_a的反函数的图象关于（　 ）

A.x轴对称　　　　　　　 B.y轴对称

C.y=x对称　　　　　　　 D.原点对称

【解析】a>0,a≠1时，y=log_ax的反函数是y=a^x,函数y=log_a的反函数为y=a^-x.而y=a^x与y=a^-x的图象关于y轴对称。

【答案】B

8.已知函数f(x+1)的定义域为(0，1)，则函数f(x)的定义域为(　　)

A.(，1)　　　　　　　　　　　　　　　 B.(1，2)

C.(0，+∞)　　　　　　　　　　　　　　　D.(,)

【解析】∵0<x<1，∴1<x+1<2,故1<x<2，∴<x<.

【答案】D

9.函数y=log₂1－x的图象是(　　)

【解析】函数y=log₂1－x可由下列变换得到：y=log₂x→y=log₂x→y=log₂x－1→y=log₂1－x.

【答案】D

10.函数f(x)=lg(3－2x－x²)的定义域为A，值域为B，则A∩B为(　　)

A.(－∞，lg4]　　　　　　　　　　　　　　　　　 B.(－3,1)

C.(－3,lg4]　　　　　　　　　　　　　　　　 D.(－1,lg4］

【解析】由3－2x－x²＞0得A={x－3＜x＜1}

由f(x)=lg［－(x+1)²+4］≤lg4

即B=(－3，lg4］.

【答案】C

第Ⅱ卷　 (非选择题　共70分)

二、填空题(本大题共4小题，每小题4分，共16分，把答案填在题中横线上)

11.已知f(x)=2^x+b的反函数为f^-1(x),若y=f^-1(x)的图象过点Q(5,2),则b=_________。

【解析】由y=2^x+b得x=log₂(y-b).

∴f^-1(x)=log₂(x-b)(x>b).

∵y=f^-1(x)的图象过（5，2），

∴2=log₂(5-b),b=1.

【答案】1

12.已知正实数a,b,c均不为1，a^x=b^y=c^z,且++=0，则abc=______.

【解析】令a^x=b^y=c^z=k>0

∴x=log_ak,y=log_bk,z=log_ck

∴++=log_ka+log_kb+log_kc=log_kabc=0

∴abc=1.

【答案】1

13.函数y=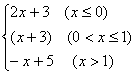的最大值是______.

【解析】此函数的图象是由y=2x+3(x≤0)表示的射线.y=x+3(0＜x≤1)表示的线段和y=－x+5(x＞0)表示的射线三部分合在一起组成的，由图象可知当x=1时，y_最大=4.

【答案】4

14.朱老师给出一个函数y=f(x),四个学生甲、乙、丙、丁各指出这个函数的一个性质：

甲：对于x∈R,都有f(1+x)=f(1－x);

乙：在(－∞,0］上是减函数；

丙：在(0，+∞)上是增函数；

丁：f(0)不是函数的最小值.

现已知其中恰有三个说得正确，则这个函数可能是______(只须写出一个这样的函数即可).

【解析】f(1+x)=f(1－x)说明x=1是f(x)图象的一条对称轴

当乙、丙都正确时，甲、丁都不正确.

当甲正确时乙，丁也正确，但丙不正确，符合这个条件的函数可以是y=(x－1)².

【答案】y=(x－1)²(注：答案不唯一)

三、解答题(本大题共5小题，共54分.解答应写出文字说明、证明过程或演算步骤)

15.(本小题满分8分)设集合A={x3－2x<5},B={x2x²+7x－15≤0},C={xx－a>1},若_R(A∩B) C,求实数a的取值范围.

【解】 A={x－1<x<4},B={x－5≤x≤},A∩B={x－1<x≤},

故_R (A∩B)={xx≤－1或x>},又C={xx－a>1}={xx<a－1,或x>a+1},因此_R (A∩B) C的充要条件是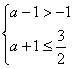解得0<a≤.

16.（本小题满分10分）设函数f(x)是定义在（-2，2）上的减函数，满足：f(-x)=-f(x),且f(m-1)+f(2m-1)>0,求实数m的取值范围。

【解】∵f(-x)=- f(x),由f(m-1)+f(2m-1)>0,得f(m-1)>-f(2m-1),即f(m-1)>f(1-2m).

又f(x)是定义在（-2，2）上的减函数，故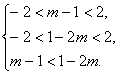解得-.

17.(本小题满分12分)已知f(x)=lgx,若当0<a<b<c时，f(a)>f(c)>f(b),试证：0＜ac＜1.

【证明】 f(x)=

若a≥1,则由f(x)在［1，+∞)上是增函数及a<b<c得f(a)<f(b)<f(c)矛盾，故0<a<1,若c≤1,

则由f(x)在(0，1)上是减函数，

0<a<b<c,知f(a)>f(b)>f(c)矛盾，故c>1,从而f(a)=－lga>f(c)=lgc即lga+lgc<0,lga<0,故0<ac<1.

18.(本小题满分12分)已知f(x)=()²(x≥1)，

(1)求f(x)的反函数f^－1(x);

(2)判断f^－1(x)的单调性.

【解】 (1)因为x≥1,所以f(x)∈［0，1)

对=,x=,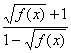

即f^－1(x)=，x∈［0,1)

(2)任取0<x₁<x₂<1

有0≤<<1

1－>0，1－>0

又f^－1(x)= =－1+

得f^－1(x₁)=－1+

f^－1(x₂)=－1+

f^－1(x₁)－f^－1(x₂)= －

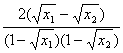=<0

∴f^－1(x₁)<f^－1(x₂)

即f^－1(x)在［0，1］上是增函数.

19.(本小题满分12分)经市场调查，某商品在近100天内其销售量和价格均是相间t的函数，且销售量近似地满足关系：g(t)=-+(t∈N*，0<t≤100)。在前40天内价格为f(t)=t+22(t∈N*，0<t≤40)；在后60天内价格为f(t)=-t+52（t∈N*，40<t≤100）。求这种商品的日销售额的最大值（近似到1）。

【解】前40天内日销售额为S=(t+22)(-t+)=-t²+t+799,

∴S=-（t-10.5）²+.

后60天内日销售额为S=(-t+52)(- t+)=∴S=(t-106.5)²-.

函数关系式为S=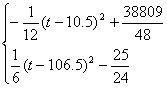由上式可知对于0<t≤40且t∈N*，当t=10或11时，S_max=809.

对于40<t≤100且t∈N*，当t=41时，S_max=714.综上得，当t=10或11时，S_max=809.