2．1　向量的概念及其表示

班级　　　　姓名　　　　学号　　　　年级　　　　学科　　　  

一、概念回顾（认真阅读课本第57,58,59页，回答下面问题）

1．　　　　　　　　　　　　　　　　 称为向量；常用　　　　　　　　　 表示，　　

记为　　　　　　 ，又可用小写字线表示为　　　　　　　　  　　　　　，

2．　　　　　　　　　　　  　　　　　称为向量的长度（或称为模），记作　　 ，

　　　　　　　　　　　　　 　　　 称为零向量，记作　　　 　　　　　　 ，

　　　　　　　　　　　　　 　　　 称为单位向量．

3．　　　　　　　　　　　　　　　　  称为平行向量，记作　　　　　　 　　 ，

　　　　　　　　　　　　　　　　  称为相等向量，记为　　　　　  　　　，

　　　　　　　　　　　　　　　　　又称为共线向量．

二、理解与应用

1．下列物理量中，不能称为向量的是　　　　　　　　　　　　　　　 （　　）

A．质量　　　　B．速度　　　　　　 C．位移　　　　　　　D．力

2．设O是正方形ABCD的中心，则向量、、、是　　（　  ）

A．平行向量　　　　　　　　　　 B．有相同终点的向量

C．相等的向量　　 　　　　　　 D．模都相同的向量

3．已知O是正方形ABCD对角线的交点，在以O，A，B，C，D这5点中任意一点为起点，另一点为终点的所有向量中，

（1）与相等的向量有　　　　　　　　　　　　 　　　　 ；

（2）与长度相等的向量有　　　　　　　　　  　　　　　；

（3）与共线的向量有　　　　　　　　　　  　　　　　　．

4．在①平行向量一定相等；②不相等的向量一定不平行；③共线向量一定相等；④相等向量一定共线；⑤长度相等的向量是相等向量；⑥平行于同一个向量的两个向量是共线向量中，不正确的命题是　　　　　　　　　  ．并对你的判断举例说明　　　　　　　　　　　　　　　　　　　　　　　　　  　　　　 ．

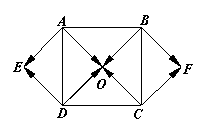5．如图，O是正方形ABCD对角线的交点，四边形OAED，OCFB都是正方形，在图中所示的向量中：

（1）与相等的向量有　 　　　　　　　　 ；

（2）写出与共线的向量有　　　　  　　　 ；

（3）写出与的模相等的向量有　　　　　　

　　　　　　　　　　  　　　　　　　　 ；

（4）向量与是否相等？答　　　　　　 ．

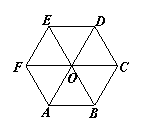6．O是正六边形ABCDE的中心，且，，，在以A，B，C，D，E，O为端点的向量中：

（1）与相等的向量有　　　　 　　　　　 ；

（2）与相等的向量有　　　　　　　　　　；

（3）与相等的向量有　　　　  　　　　　 ．
7．在如图所示的向量，，，，中（小正方形的边长为1），是否存在：

（1）是共线向量的有　　　　　　　　　　　　  ；

（2）是相反向量的为　　　　　　　　　　　　  ；

（3）相等向量的的　　　　　　　　　　　　　  ；

（4）模相等的向量　　　　　　　　　  　　　　．

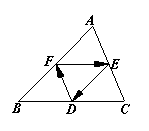
8．如图，△ABC中，D，E，F分别是边BC，AB，CA的中点，在以A、B、C、D、E、F为端点的有向线段中所表示的向量中，

（1）与向量共线的有　　　　　　　　 　　　　　．

（2）与向量的模相等的有　　　　　　　　　　　 ．

（3）与向量相等的有　　　　　　　 　　　　　　．

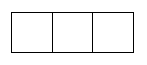
9．如图，以1×3方格纸中的格点为起点和终点的所有向量中，有多少种大小不同的模？有多少种不同的方向？

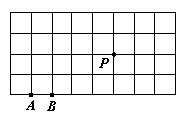
10．如图，中国象棋的半个棋盘上有一只“马”，开始下棋时，它位于A点，这只“马”第一步有几种可能的走法？试在图中画出来．若它位于图中的P点，这只“马”第一步有几种可能的走法？它能否从点A走到与它相邻的B？它能否从一交叉点出发，走到棋盘上的其它任何一个交叉点？

三、方法总结：