高一年级数学第二章单元测试
姓名:___________ 班级:____________ 得分：_____________
一选择题：（每题5分，共60分）
1．如果(x,y)在映射f下的象是(x+y,x-y)，那么(1,2)在f下的原象是 （ ）
A.(
)B.(
) C.(
) D.(
)
2。求下列函数中，值域是
的函数是
（ ）
A．
B。 
C。
D。
3．若将函数
的图象向下平移5个单位，再向右平移5个单位时，与原数的反函数的图象重合，则m等于
（ ）
A. 6 B.
4．若指数函数y=f(x)的反函数的图象经过点（2，-1），则函数的解析式为 （ ）
A．
B。
C。
D。
5．函数
的单调递减区间为
（
）
A. 
B. 
C. 
D. 
6．函数
的图象与x轴有交点，m的范围是
（ ）
A. 
B. 
C. 
D. 
7．设
，计算
的结果是
（ ）
A. 
B. 
C. 
D. 
8．若
与
在区间[1，2]上都是减函数，则a的取值范围是（ ）
A. 
B. 
C. 
D. 
9．函数
的定义域是
（ ）
A. 
B. 
C. 
D. 
10．函数
是单调函数的充要条件是
（ ）A. 
B. 
C. b>0
D. b<0
11．设
,则
（ ）
A. 
B. 
C. 
D. 
12．若f(x)与g(x)都是定义在实数集R上的函数，且方程
有实数根，则
不可能是
（ ）A. 
B. 
C. 
D. 
答题卡
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
一．填空题：（4分
4=16分）
1．函数
(a>0且
)在区间[1，2]上的最大值比最小值大
，则a的值为________;
2．函数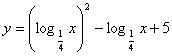
的值域为_________;
3．已知函数
的定义域为
,则
的定义域为________;
4．下列命题：
①若
有意义，则
；
②因为
在上是增函数，所以
在上也是增函数；
③函数
在
上是减函数；
④函数
与的图象重合；
其中正确的命题的序号是___________（少选、多选本踢都不给分）
三、解答题（第6大题14分，其余每题12分）
1．已知函数
（1）求函数的定义域与值域；
（2）求函数的单调区间。
2．设函数
（1）求;
（2）证明：
;
（3）当a>1时，求满足
的x的取值范围;
（4）当a>1时，讨论的单调性.
3．某出租公司拥有汽车100辆，当每辆车的月租金为3000元时，可全部租出。当每辆车的租金每增加50元时，未租出的车将会增加一辆，租出的车每辆每月需要维护费150元，未租出的车每辆每月需要维护费50元。
（1）当每辆车的月租金为3600元时，能租出多少车辆？
（2）当每辆车的月租金为多少元时，出租公司的月收益量最大？最大月收益是多少？
4．已知的f(x)定义在上的单调递增函数，且对定义域内的任意x，都有f(xy)=f(x)+f(y)且f(2)=1，求使不等式
成立的的取值范围。
5．已知二次函数
（a,b是常量，且
）f(2)=1且方程f(x)=x有等根。
（1）求f(x)的解析式；
（2）是否存在常数p,q(p<q)，使得f(x)的定义域和值域分别是[p,q]和[2p,2q]，如存在，求出p,q的值。如果不存在，说明理由。
6、是否存在实数a，使得函数
在[2，4]上增函数？若存在，指出a的取值范围；若不存在，说明理由。