高一数学第一次联考试卷
说明:1、本试卷分第I、II 两卷,共150分。考试时间100分钟
2、请将选择题答案填入第II卷前的答题表中,考试结束时,只交第II卷。
第Ⅰ卷(选择题 共60分)
一、选择题(本大题共12个小题,每小题5分,共60分)
1、下列集合中,表示同一集合的是
A、M= {(3,2)},N={(2,3)} B、M={3,2} ,N={2,3}
C、M={(x,y) x+y=1},N={yx+y=1} D、M={3,2},N={(2,3)}
2、设集合P={1,2,3,4},Q={x x≤2}则P![]() Q等于
Q等于
A、{1,2} B、{3,4} C、{1} D、{-2,-1,0,1,2}
3、若不等式ax+2<6的解集为{x—1<a<2},则实数a等于
A、8 B、2 C、-4 D、-8
4、不等式x—1+x—2≤3的最小整数解是
A、-1 B、0 C、1 D、2
5、设x是实数,那么x<5成立的一个必要非充分条件是
A、x<5 B、x<4 C、x2<25 D、0<x<4
6、设M={0,1,2,3,4} ,N={x x=![]() ,a∈M,b∈M},则M
,a∈M,b∈M},则M![]() N的子集个数是
N的子集个数是
A、15 B、16 C、31 D、32
7、不等式x(1—2x)>0的解集是
A、 {xx< ![]() }
B、{xx<
}
B、{xx< ![]() 且x≠0 }
且x≠0 }
C、{xx> ![]() }
D、{x0<x<
}
D、{x0<x< ![]() }
}
8、已知A={x x—2<3} ,B={x x2—ax<a—x}若A∪B=A,则a的取值范围是
A、-1≤a≤5 B、-1<a<5 C、-1≤a<5 D、-1<a≤5
9、a>0,使不等式x—4 + x—3<a在R上解集不是空集的a的取值范围是
A、0<a<1 B、 0≤a<1 C、1<a D、1≤a
10、设全集∪=R,集合M={x —x2+2005x+2006<0},P={x x—2005<a(a为常数)}且-1∈P,则M与P满足
A、M∪P=R B、(C∪ M)∪P=R
C、M∪(C∪ P)=R D、(C∪ M)∪(C∪ P)=R
11、设集合A={x x<4,B={xx2—4x+3>0}则集合{xx∈A且x![]() A
A![]() B}等于
B}等于
A、{x —4<x<1或3<x<4} B、{x1<x<3}
C、{x —4≤x≤1或3≤x≤4} D、{x1≤x≤3}
12、数集M={ x m ≤x≤m+![]() } ,N={x n —
} ,N={x n —![]() ≤x≤ n }且M、N都为集合{x0≤x≤ 1}的子集,若 b — a叫做集合{x a
≤ x ≤b }的“长度”,那么集合M
≤x≤ n }且M、N都为集合{x0≤x≤ 1}的子集,若 b — a叫做集合{x a
≤ x ≤b }的“长度”,那么集合M![]() N的长度的最小值为
N的长度的最小值为
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
高 一 数 学第一次联考试卷
| 题号 | 一 | 二 | 三 四 五 六 七 | 总分 | |||||
| 17 | 18 | 19 | 20 | 21 | 22 | ||||
| 得分 | |||||||||
请将选择题答案填入下表:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
第Ⅱ卷(非选择题 共90分)
| 得 分 | |
| 评卷人 |
二、填空题(本大题共4个小题,每小题4分,共16分)
13、对不等式x—a>b①当b<0时解集为R,②当b=0时解集为{a},③当b>0时,解集为{x x<a—b 或x>a +b },其中错误答案的序号为:_____________________
![]() 14、设A、B是两个集合,命题C是这样构成的:它的递命题的条件是“A
14、设A、B是两个集合,命题C是这样构成的:它的递命题的条件是“A![]() B=A”,它的否命题的条件是“A B”,则命题C是:______________ ____________
B=A”,它的否命题的条件是“A B”,则命题C是:______________ ____________
15、已知A={x —2 ≤x ≤4},B{x x>a }若A![]() B=φ,A∪B≠B,则A的取值范围是:___________________________________________
B=φ,A∪B≠B,则A的取值范围是:___________________________________________
16、设自然数集N为全集,已知A1、A2、B是它的三个互不相等的子集,其中B={xx=6m,m∈N},若A1 、A2是满足使得“x∈Ai(i=1、2)”是“x∈B”的必要非充分条件的两个集合,用描述法写出A1= ,A2=___________.
三、解答题(本大题共6小题,17-21题每题12分,22题14分,共74分。)
| 得 分 | |
| 评卷人 |
17、在直角坐标系中,若点(2x+3-x2, ![]() )在第四象限,求x的取值范围
)在第四象限,求x的取值范围
| 得 分 | |
| 评卷人 |
18、解不等式ax2+2a2x-3a3>0
| 得 分 | |
| 评卷人 |
19已知c>0,设P:方程x2 — 2cx + c=0没有实数根;q:不等式x+2x+2c>0的解集为R,如果命题P或q为真,命题P且q为假,求c的取值范围。
| 得 分 | |
| 评卷人 |
20、约定“![]() ”与“
”与“![]() ”是两个运算符号,其运算法则如下:
”是两个运算符号,其运算法则如下:
对任意的a,b∈R,有a![]() b=ab a
b=ab a![]() b=
b=![]()
设∪={cc=(a![]() b)+(a
b)+(a![]() b),-2<a≤b<1,a,b∈Z}
b),-2<a≤b<1,a,b∈Z}
A={dd=2(a![]() b)+
b)+ ![]() ,-1<a<b<2,a,b∈Z}
,-1<a<b<2,a,b∈Z}
求:C∪ A
| 得 分 | |
| 评卷人 |
21、已知集合A={x x —![]() (a+1)2 ≤
(a+1)2 ≤![]() (a-1)2}
(a-1)2}
B={x2≤x≤3a+1}
(1)是否存在实数a,使得A是一个单元素的集合?若存在,求出这样的集合A,若不存在,请说明理由。
(2)若存在实数a,使得A![]() B,试求这样的a的取值范围。
B,试求这样的a的取值范围。
| 得 分 | |
| 评卷人 |
22、已知a>0且a≠1,x-1<ax
(1)解上述不等式
(2)求使上述不等式的解集中恰有两个整数的a的取值。
高一年级月考数学参考答案
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | A | C | B | A | D | B | A | C | A | D | C |
二、填空题
13、②
14、设A、B是两个集合,若A![]() B,则A
B,则A![]() B=A
B=A
15、a≥4
16、A1={xx=2k,k∈N}, A2={xx=3n,n∈N}
三、解答题
17、∵点(2x+3-x2 , ![]() )在第四象限
)在第四象限
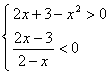 | |||
| |||
∴
|
|
|
当a>0时, 原不等式![]() (x+3a)(x-a)>0
(x+3a)(x-a)>0
∴x>a或x<-3a
|
当a<0时,原不等式![]() (x+3a)(x-a)<0
(x+3a)(x-a)<0
∴a<x<-3a
|
19、∵方程x2 — 2cx + c=0没有实数根
∴ △= 4c2-4c<0, 解得0<c<1
|
命题P为假时, c≥1
由不等式x2+2x+2c>0的解集为R,得:
△=4-8c 解的:c>![]()
所以命题q真时, c>![]()
|
因为命题P或q为真,命题P且q为假。
所以P、q必定是一真一假。
当P真q假时,0<c≤![]()
|
|
20、由-2<a≤b<1 且a,b∈Z可知
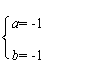 | 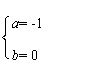 | ||||
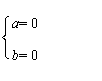 | |||||
或 或
分别代入c=(a![]() b)+(a
b)+(a![]() b)=ab+
b)=ab+![]() 得 c=1或 —
得 c=1或 —![]() 或0
或0
|
由-1<a<b<2且a,b∈Z ,得 a=0,b=1
此时d=2(a![]() b)+
b)+![]() = —
= — ![]()
|
∴C∪ A={1,0}
21、(1)由x-![]() (a+1)2≤
(a+1)2≤![]() (a-1)2可得
(a-1)2可得
|
即A={x2a≤x≤a2+1}
|
(2)∵A![]() B
B
|
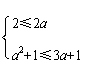 ∴
∴
∴1≤a≤3
|
22、(1)∵a>0且a≠1
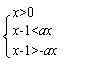
|
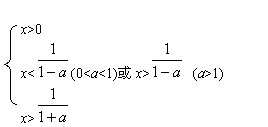 | |||||||
|
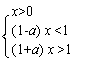
![]()
![]()
∴a>1时,不等式解集为{x x>![]() }
}
|
(2)由题设知,应有0<a<1
又∵1∈ {x ![]() <x<
<x<![]() }
}
|
解得: ![]() <a≤
<a≤![]()
|
