高一数学第一学期教学质量检测试卷

题号	1-10	11-14	15	16	17	18	总分
得分

说明：不能使用计算器；本试卷满分100分，在90分钟内完成

一、选择题：（本大题共10小题，每小题4分，共40分）

题号	1	2	3	4	5	6	7	8	9	10
答案

每题的4个答案中，只有一个是正确的，请把选出的答案编号填在上面的答题表中

1、设U={至少有一组对边平行的四边形}，A={平行四边形}，B={梯形}，则下列关系不正确的是

　  A、A∪B=U　　 　 B、A∩B=Φ 　　C、BU　　　　　D、BA

2、若集合A、B、C满足，则A与C的关系是

A、　　　　 B、　　　　C、　　　　 D、

3、若命题p是真命题，非q是真命题，则下列形式命题中是真命题的是

A、非p　　 　　　B、q　　 　　　　C、p且q　　　　　D、p或q

4、设a是实数，那么a<5成立的一个必要非充分条件是

A、a<4　 　　　　B、a<5　 　　　　C、a²<25　 　　　 D、-5<a<5

5、方程mx²+(m+1)x+m=0有两个不相等的实根，则m的取值范围是

A、-<m<1　　　　　　　　　　　　B、-1<m<　　

C、-<m<1且m0　 　　　　　　　D、-1<m<且m0

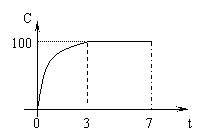6、芒幕电子公司7年来，生产VCD机总产量C（万台，即前t年年产量的总和）与时间t（年）的函数关系如图，下列四种说法

① 前3年中，产量增长的速度越来越快；

② 前3年中，产量增长的速度越来越慢；

③ 第3年后，这种产品停止生产；

④ 第3年后，年产量保持为100万台.

其中说法正确的是：

A、①与③　B、②与③　 C、②与④　 D、①与④　　

7、如果函数y=mx+2与y=3x-n的图象关于直线y=x对称，则

A、m=，n=6　　 B、m=，n= -6　　C、m=3，n= -2　　D、m=3，n=6

8、已知lgm=b-2lgn，那么m等于

A、　　　　　  B、　　　 　　 C、b-2n　　　　  D、

9、设{a_n}递增等差数列，前三项的和为12，前三项的积为48，则它的首项为

A、1　　　　 　　 B、2　　 　　　　　C、4　　 　　　　 D、6

10、若{a_n}是等比数列，且a_n>0，a₂a₄+2a₃a₅+a₄a₆=25，则a₃+a₅的值为

A、5　　　　　　　B、10　　　　　　  C、15　　　　　　 D、20

二、填空题：（本大题共4小题，每小题4分，共16分）

11、已知函数f (x)在（0，+∞）上为减函数，且在R上满足f (-x)=f (x)，则f (-2)、f (-5)、f (π)三个数的按从小到大依次排列为__________________________.

12、函数y=定义域是______________________.

13、若数列{a_n}满足a_n+1=且a₁= 0，则a₇=___________.

14、下列命题：

　　①若元素（x，y）对应映射f下的元素（x+y，x-y），则在f下的（1，-3）的原象为（-2，4）；

②函数f(x)=在[0，1）上为增函数；

　　③函数y=（x≥1）的反函数为（x≤0）；

④“全等三角形的面积相等”的否命题；

其中假命题为_____________. （填写命题的序号）

三、解答题：（第15、16题每题10分，第17、18题每题12分，共44分）

15、已知全集U＝{x x-7x+10≥0}，A={x x -4 >2} ，B={x ≥0}

　　求：C _UA，AB

解：

16、数列{a_n}，S_n为它的前n项的和，已知a₁= -2，a_n+1 = S_n，当n≥2时，求：a_n 和S_n.

解：

 

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

17、已知正方形ABCD的边长为2，有一动点M从点B出发沿正方形的边运动，路线是BCDA . 设点M经过的路程为x，△ABM的面积为S.

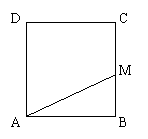求函数S=f(x)的解析式及其定义域.

解：

18、已知函数及函数（a，b，c∈R），若a>b>c且a+b+c=0.

（1）证明：f(x)的图像与g(x)的图像一定有两个交点；

（2）请用反证法证明：；

（3）若f(x)的图像与g(x)的图像的两个交点为A、B，试求出 x_A -x_B 的取值范围.