南宁二中高一数学两角和与差的三角函数测试题

一、选择题：

1、函数y=sinxcosx+ cos²x－ 的最小正周期是　　　　　　　　　　　　　　　　　　　　　 （　　）

　　A．π　　　　　　　　B．2π　　　　　　　 C．　　　　　  D．

2、函数f(x) = 的值域为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　A．　　 　　　B．　　　 　 C．[－4,0]　　　　　 D．[0,4]

3、设t = sinθ+cosθ,且sin³θ+cos³θ<0,则t的取值范围是　　　　　　　　　　　　　　　　　　（　　）

　 　A．[－ ,0]　　 　　　　　　　　　　　　　　　　　　　 B．(－1,0)∪(1,  )

　　　 C．[－ ,  ]  　　　　　　　　　　　　　　 D．(－,0)∪( ,+ ∞)

4、已知tan(α+β) = , tan(β－ )= ,那么tan(α+ )为　　　　　　　　　　　　　　 （　　）

　 　A．　　　　　 B．　　　　　 C．　　　　　 D．

5、已知关于x的方程2cosx+6sinx+1=0的两根分别为α、β,且α、β∈(0,2π),α≠β,则

sin(α+β)等于　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

A．　　　 　　　　　　　　　　　　　　　　　　　　 B．　　　　 　　

C．　　　　　　　　　　　　　　　　　　　　　　　　 D． 

6、设α，β是一个钝角三角形的两个锐角，下列四个不等式中不正确的是　　　　　　（　　）

　　　 A．tanαtanβ<1　　　　　　  　　　　　　　B．sinα+sinβ<　　　

　　　 C．cosα+cosβ>1　　　　　　　  　　　 D．tan(α+β)<tan　　　

7、在ΔABC中，3sinA＋4cosB＝6，4sinB＋3cosA＝1，则C的大小为　　　　　　　　　　（　　）

　　　 A．　　　　 　　　B．　　　　  　C．或　　　 D．或

8、 已知函数f(x)=2asin²x－2 sinxcosx+a+b(a<0)的定义域是[0,  ],值域为[－5,1],则a、b值　　　　 分别为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　 　A．a=2, b=－5　　 B．a＝－2,b=2　　　C．a=－2, b=1　　 D．a=1,b=－2

二、填空题：

9、设α、β均为锐角，cosα＝ ，cos(α+β）=－ ,则cosβ＝＿＿＿.

10、 tan300°+cot405°的值为_______.

11、(1+ tanα)(1+tanβ)= 4,且α,β都是锐角,则α+β=______.

12、化简： = ________.

三、解答题：

13、已知α,β∈(0,π),且tanα,tanβ是方程x²－5x+6=0的两根.

　　①求α+β的值.

　　②求cos(α－β)的值.

14、已知求.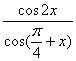

15、是否存在锐角α和β，使得①α+2β=； ②tanβ=(2－ )cot 同时成　　　　 立？若存在,请求出α和β的值；若不存在,请说明理由.

16、二次函数f(x)=x²+bx+c(b,c∈R),已知无论α,β为任何实数,f(sinα)≥0,f(2+cosβ)≤0.

　　①求证：b+c= －1.

　　②求证：c≥3

　　③若f(sinα)的最大值为8,求f(x)的解析式.

　　　　　　　　　　　　　　　　　

　　　　　　　

参考答案

两角和与差的三角函数

一、AAACC　DAC

二、（9）　 （10）　　（11）　　（12）　

三、（13）①由根与系数的关系得：

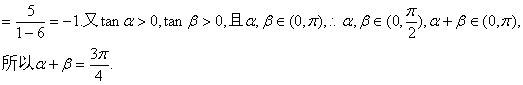
②由（1）得

由（2）得

的两个根，解得：

②

③

①

①②