普宁英才侨中05-06学年高一数学必修1《函数的应用》复习题
班级 姓名 座号 得分
一、选择题。(本题共12小题,每小题5分,共60分)
1、下列函数有2个零点的是( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
2,方程x-1=lgx必有一个根的区间是( )
A, (0.1 ,0.2) B,(0.2,0.3) C,(0.3,0.4) D,(0.4,0.5)
3,函数y=(0.5)x与函数y=lgx的图象的交点的横坐标(精确到0.1)约是( )
A,1.3 B,1.4 C,1.5 D,1.6
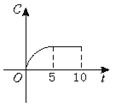
4,某工厂10年来某种产品总产量C与时间t(年)的函数关系如下图所示,下列四种说法,其中说法正确的是( )
①前五年中产量增长的速度越来越快 ②前五年中产量增长的速度越来越慢 ③第五年后,这种产品停止生产 ④第五年后,这种产品的产量保持不变
 A.②③ B.②④
C.①③ D.①④
A.②③ B.②④
C.①③ D.①④
5下图△ABC为等腰直角三角形,直线l与AB相交且l⊥AB,直线l截这个三角形所得的位于直线右方的图形面积为y,点A到直线l的距离为x,则y=f(x)的图象大致为( )


6,已知实数a、b、c是图象连续不断的函数y=f(x)定义域中的三个数,且满足a<b<c
,f(a).f(b)<0, f(b).f(c)<0,则函数y=f(x)在区间(a,c)上的零点个数为( )
A, 2 B,奇数 C,偶数 D,至少是2
7.已知镭经过100年,剩留原来质量的95.76%,设质量为1的镭经过x年的剩留量为y,则y与x的函数关系是( )
A.y={0.9576}![]() B.y={0.9576}100x
B.y={0.9576}100x
C.y=(![]() )x
D.y=1-(0.0424)
)x
D.y=1-(0.0424)![]()
8某人2003年1月1日到银行存入一年期存款a元,若按年利率为x,并按复利计算,到2008年1月1日可取回款 ( )
A.a(1+x)5元 B.a(1+x)6元 C.a(1+x5)元 D.a(1+x6)元
9已知0<a<1,则方程ax=logax的实根个数是 ( )
A.1个 B.2个 C.3个 D.1个或2个或3个
10,若方程ax-x-a=0有两个解,则a的取值范围是( )
A, (0,1) B, (1,+∞) C,(0,+∞) D,(-1,0)
11, 设![]() ,则x的值的范围是( )
,则x的值的范围是( )
A.-2<x<-1 B.-3<x<-2 C.-1<x<0 D.0<x<1
12, 用二分法计算![]() 在
在![]() 内的根的过程中得:
内的根的过程中得:
![]() ,
,![]() ,
,![]() ,则方程的根落在区间( )
,则方程的根落在区间( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
二,填空题。(本题共4小题,每小题5分,共20分)
13, 工厂生产某种产品的月产量y与月份x满足关系y=a·(0.5)x+b,现已知该厂今年1月、2月生产该产品分别为1万件、1.5万件.则此厂3月份该产品的产量为__________.
14,若方程x3-x+1=0在区间(a,b)(a,b是整数,且b-a=1)上有一根,则a+b=________.
15, 国家规定个人稿费纳税办法为:不超过800元的不纳税;超过800元而不超过4000元 的按超过800元的14%纳税;超过4000元的按全稿酬的11%纳税.某人出版了一书共 纳税420元,这个人的稿费为____元。
16, 已知函数![]() 的图象是连续不断的,有如下
的图象是连续不断的,有如下![]() 对应值表:
对应值表:
|
| -2 | -1 | 0 | 1 | 2 | 5 | 6 |
|
| -10 | 3 | 2 | -7 | -18 | -3 | 38 |
则函数![]() 在区间
有零点。
在区间
有零点。
三、解答题(本大题共5小题,共70分.解答应写出文字说明,证明过程或演算步骤)
17,(本小题共12分)借助计算器或计算机,用二分法求方程(x+1)(x-2)(x-3)=1的近似解(精确度0.1)
18,(本小题共12分)截止到1999年底,我国人口约13亿,如果经过30年后,我国人口不超过18亿,那么人口年平均增长率不应超过多少(精确到0.01)?
19,(本小题共14分)一个体户有一种货,如果月初售出可获利100元,再将本利都存入银行,已知银行月息为2.4%,如果月末售出可获利120元,但要付保管费5元,问这种货是月初售出好,还是月末售出好?
20,(本小题共14分)某种商品现在定价每年p元,每月卖出n件,因而现在每月售货总金额np元,设定价上涨x成,卖出数量减少y成,售货总金额变成现在的z倍.(1)用x和y表示z.
(2)若y=![]() x,求使售货总金额有所增加的x值的范围.
x,求使售货总金额有所增加的x值的范围.
21,(本小题共18分)(1)某工厂计划出售一种产品,经销人员并不是根据生产成本来确定这种产品的价格, 而是通过对经营产品的零售商对于不同的价格情况下他们会进多少货进行调查.通过调查确定了关系式P =-750x+15000 ,其中P为零售商进货的数量,x为零售商愿意支付的每件价格.现估计生产这种产品每件的材料和劳动生 产费用为4元,并且工厂生产这种产品的总固定成本为7000元(固定成本是 除材料和劳动费用外的其他费用),为获得最大利润,工厂应对零售商每件 收取多少元?
(2)某商品在最近100天内的价格f(t)与时间t的函数关系是:
|
f(t) =
销售量g(t)与时间t的函数关系是: g(t) = -![]() t +
t + ![]() (0≤t≤100 , t ∈N), 求这种商品的日销售额S(t)的最大值.
(0≤t≤100 , t ∈N), 求这种商品的日销售额S(t)的最大值.
普宁英才侨中05-06学年高一数学必修1《基本初等函数Ⅰ》复习题参考答案
一、选择题。(本题共12小题,每小题5分,共60分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | A | A | D | A | C | D | A | A | B | B | A | D |
二,填空题。(本题共4小题,每小题5分,共20分)
13, 1.75万件 14, -3 15, 3800 16, (-2,-1) , (0,1) , (5,6)
三、解答题(本大题共5小题,共70分.解答应写出文字说明,证明过程或演算步骤)
17,近似解为-0.9375 (详见必修1教师用书P86第3题答案)
18,不超过1% (详见必修1教师用书P104第11题答案)
19,解:设这种货的成本费为a元,则若月初售出,到月末共获利润为:
y1=100+(a+100)×2.4%
若月末售出,可获利y2=120-5=115(元)
y2-y1=0.024a-12.6=0.024(a-525)
故当成本大于525元时,月末售出好;成本小于525元时,月初售出好.
20,解:(1)npz=p(1+![]() )·n(1-
)·n(1-![]() )
)
∴z=![]()
(2)当y=![]() x时,z=
x时,z=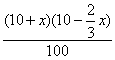
由z>1,得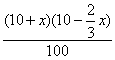 >1
>1
x(x-5)<0,∴0<x<5
21,解:(1)设总生产成本为Q元,总收入为S元,总利润为y元,y=S-Q,Q=4P+7000=4(-750x+15000)+7000,即Q=-3000x+67000,S=Px(-750x+150000)x=-750x2+15000x.∴y=-750x2+18000x-67000(x>0)即y=-750(x-12)2+41000.当x=12,ymax=41000.答:工厂应对零售商每件收取12元,才能获得最大利润.
(2)S(t)=f(t)g(t),即s(t)的最大值.只是f(t)是分段函数.解:S(t)=f(t)g(t)当
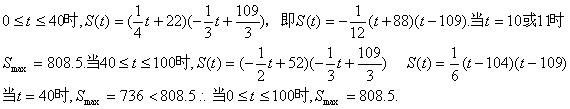 答:在最近的100天内,这种商品的日销售额的最大值为808.5.
答:在最近的100天内,这种商品的日销售额的最大值为808.5.