高中数学必修3检测题
2004学年第二学期
高中数学必修3第一章(统计)检测题
班级 姓名 学号
一、选择题：（本题共10小题，每小题3分，共30分，在每小题给出的四个选项中，只有一项是符合题目要求的）
1．某单位有老年人28人，中年人54人，青年人81人．为了调查他们的身体状况，需从他们中抽取一个容量为36的样本，最适合抽取样本的方法是( )．
A．简单随机抽样 B．系统抽样
C．分层抽样 D．先从老年人中剔除一人，然后分层抽样
2．10名工人某天生产同一零件，生产的件数是15，17，14，10，15，17，17，16，14，12．设其平均数为a，中位数为b，众数为c，则有( )．
A．a>b>c B．b>c>a C．c>a>b D．c>b>a
3．下列说法错误的是( )．
A．在统计里，把所需考察对象的全体叫作总体
B．一组数据的平均数一定大于这组数据中的每个数据
C．平均数、众数与中位数从不同的角度描述了一组数据的集中趋势
D．一组数据的方差越大，说明这组数据的波动越大
4．下列说法中，正确的是( )．
A．数据5，4，4，3，5，2的众数是4
B．一组数据的标准差是这组数据的方差的平方
C．数据2，3，4，5的标准差是数据4，6，8，10的标准差的一半
D．频率分布直方图中各小长方形的面积等于相应各组的频数
5．从甲、乙两班分别任意抽出10名学生进行英语口语测验，其测验成绩的方差分别为S12= 13.2，S22=26．26，则( )．
A．甲班10名学生的成绩比乙班10名学生的成绩整齐
B．乙班10名学生的成绩比甲班10名学生的成绩整齐
C．甲、乙两班10名学生的成绩一样整齐
D．不能比较甲、乙两班10名学生成绩的整齐程度
6．下列说法正确的是( )．
A．根据样本估计总体，其误差与所选择的样本容量无关
B．方差和标准差具有相同的单位
C．从总体中可以抽取不同的几个样本
D．如果容量相同的两个样本的方差满足S12<S22，那么推得总体也满足S12<S22是错的
7．某同学使用计算器求30个数据的平均数时，错将其中一个数据105输人为15，那么由此求出的平均数与实际平均数的差是( )．
A．3.5 B．-3 C．3 D．-0.5
8．在一次数学测验中，某小组14名学生分别与全班的平均分85分的差是：2，3，-3，-5，12，12，8，2，-1，4，-10，-2，5，5，那么这个小组的平均分是( )分．
A．97.2 B．87.29 C．92.32 D．82.86
9．某题的得分情况如下：其中众数是( )．
| 得分/分 | 0 | 1 | 2 | 3 | 4 |
| 百分率/(％) | 37.0 | 8.6 | 6.0 | 28.2 | 20.2 |
A．37.0％ B．20.2％ C．0分 D．4分
10．如果一组数中每个数减去同一个非零常数，则这一组数的( )．
A．平均数不变，方差不变 B．平均数改变，方差改变
C．平均数不变，方差改变 D．平均数改变，方差不变
二、填空题：（本题共4小题，每小题3分，共12分，请把答案填写在答题纸上）
11.一个公司共有240名员工，下设一些部门，要采用分层抽样方法从全体员工中抽取一个容量为20的样本．已知某部门有60名员工，那么从这一部门抽取的员工人数是 。
12．常用的统计图表有： 。
13．常用的抽样方法有： 。
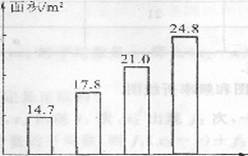14．(2002年新课程卷文第13题)据新华社
2002年3月12日电，1985年～2000年我 25.0
国农村人均居住面积如图所示，其中，从 20.0
年到 年的五年间增长最快． 15.0
1985 1990 1995 2000
三、解答题：（本题共6小题，共58分，解答应写出文字说明，证明过程或演算步骤.）
15．(6分)某展览馆22天中每天进馆参观的人数如下：
180 158 170 185 189 180 184 185 140 179 192
185 190 165 182 170 190 183 175 180 185 148
计算参观人数的中位数、众数、平均数、标准差．
【解】：
16．(7分)在相同条件下对自行车运动员甲、乙两人进行了6次测试，测得他们的最大速度(单位：m/s)的数据如下：
| 甲 | 27 | 38 | 30 | 37 | 35 | 31 |
| 乙 | 33 | 29 | 38 | 34 | 28 | 36 |
试判断选谁参加某项重大比赛更合适
【解】：
17．(12分)为了解某地初三年级男生的身高情况，从其中的一个学校选取容量为60的样本(60名男生的身高)，分组情况如下：
| 分组 | 147.5～155.5 | 155.5～163.5 | 163.5～171.5 | 171.5～179.5 |
| 频数 | 6 | 2l | m | |
| 频率 | a | 0.1 |
(1)求出表中a，m的值． (2)画出频率分布直方图和频率折线图
【解】：
18．(8分) 某赛季甲、乙两名篮球运动员每场得分情况如下：
甲的得分：12 15 24 25 3l 31 36 36 37 39 44 49 50
乙的得分：8 13 14 16 23 26 28 33 38 39 51
请你用不同的方式(统计图表)分别表示此赛季甲、乙两名篮球运动员得分情况．
【解】：
19．(15分)某连锁经营公司所属5个零售店某月的销售额和利润额资料如下表
| 商店名称 | A | B | C | D | E E |
| 销售额(x)/千万元 | 3 | 5 | 6 | 7 | 9 9 |
| 利润额(y)/百万元 | 2 | 3 | 3 | 4 | 5 |
(1)画出销售额和利润额的散点图．(2)若销售额和利润额具有相关关系，用最小二乘法计算利润额y对销售额x的回归直线方程．(3)对计算结果进行简要的分析说明．
【解】：
20．(10分)回答下列问题：
(1)如果数据x1，x2，…，xn的平均数是
，那么(x1-)+( x2-)+…+(xn-)=0总成立吗？
(2)一组数据的方差一定是正数吗?
(3)已知在n个数据中，x1出现f1次，x2出现f2次，…，xk出现fk次，(f1+…+fk =n)，是这n个数的平均数，则f1 (x1-)+ f2 (x2-)+…+fk (xk-)=0总是成立吗?
(4)为什么全部频率的累加等于1?
【解】：
答 案
一、 选择题：
1、 D 2、D 3、B 4、C 5、A 6、C 7、B 8、B 9、C 10、D
二、 填空题：
11、5
12、象形统计图、条形统计图、扇形统计图、折线统计图、茎叶图、频率分布图、频率分布直方图、频率折线图
13、简单随机抽样、分层抽样、系统抽样
14、1995，2000
三、解答题：
15、181，185，177，13.66
16、
＝33，
＝33
＞
，乙的成绩比甲稳定，应选乙参加比赛更合适
17、（1）a=0.45，m=6 （2）略
18、略 19、（1）略 （2）y=0.5x+0.4 （3）略 20、略
2004学年第二学期
高中数学必修3第二章（算法）检测题
班级 姓名 学号
一、选择题：（本题共12小题，每小题3分，共36分，在每小题给出的四个选项中，只有一项是符合题目要求的）
1．程序框图中表示判断的是( )．
A． B． C． D．
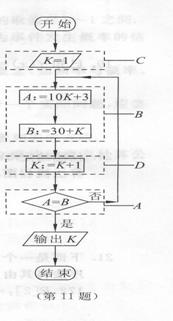
2．阅读流程图，则输出的结果是( )．
A．4 B．5 C．6 D．13
 | |||||
 | |||||
 | |||||
3．用冒泡排序法从小到大排列数据{13，5，9，10，7，4)，需要经过( )趟排序才能完成．
A．4 B．5 C．6 D．7
4．在repeat语句的一般形式中有“until A”，其中A是( )．
A．循环变量 B．循环体 C．终止条件 D．终止条件为真
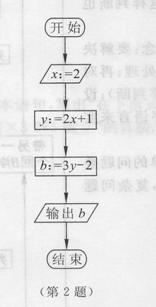
5．上图中所示的是一个算法的流程图，已知a1＝3，输出的b＝7，则a2的值是( )．
A．11 B．17 C．0.5 D．12
6．已知7163＝209×34+57，209＝57×3+38，57＝38×l+19，38＝19×2。根据上述系列等式，确定7163和209的最小公约数是( )．
A．57 B．3 C．19 D．34
7．条件语句的一般形式是“if A then B else C”，其中B表示的是( )．
A．满足条件时执行的内容 B．条件语句
C．条件 D．不满足条件时执行的内容
8．将两个数a＝8，b＝17交换，使a＝17，b＝8，使用赋值语句正确的一组是( )．
A．a：＝b；b：＝a B．c：＝b；；b：b：＝a；a：＝c
C．b：＝a；a：＝b D．a：＝c；c：＝b； b：=a
9．已知R[i]=i，i=1，2，…，10，11。试用计算机语言，将R[8]，R[9]，R[10]向后移一个位置，使R[8]空出来，使用语言正确的一组是( )．
A．R[11]：=R[l0]；R[l0]：=R[9]；R[9]：=R[8]
B．R[8]：=R[9]；R[9]：=R[l0]；R[l0]：=R[11]
C．R[11]：=R[10]；R[9]：=R[8]；R[10]：=R[9]
D．R[11]：=R[l0]；R[9]：=R[10]；R[9]：=R[8]
10．一个无序列的数据列：{a1，a2，a3，a4，a 5，a6，a 7，a8}，按有序列插入法，试计算理论上要经过( )次有序列插入才能排成一个有序列．
A．最多7 B．最少8 C．最多8 D．最少7
11．阅渎流程图（见第一页图），则循环体是( )部分．
12．7x+3y＝46的正整数解有( )组．
A．0 B．1 C．2 D．3
二、填空题：（本题共4小题，每小题3分，共12分，请把答案填写在答题纸上）
13. 156，126，60三个数的最大公约数是 。
14．运用赋值语句，写出当x= -10时，求多项式x3+5x2+360的值的算法如下：
。
15．已知一个班的人数在30到56人之间，现在按3列排，多出一人，按5列排，多出3人，按7列排，多出1人，则这个班有 人．
16．读程序： Begin
Input“x：=”；x
If x≥2， then y：=
Else y：=x+1；
Print y；
End．
现在输入x的初值为π，则程序运行的结果为 。
三、解答题：（本题共6小题，共52分，解答应写出文字说明，证明过程或演算步骤.）
17．(6分) 已知两点的坐标分别为A(x1，y1)，B(x2，y2)，设计算法求两点间的距离。
【解】：
18．(6分) 画出算法流程图，求出方程ax = b的解
【解】：
19．(10分) 已知
设计算法和流程图，求f(x)的值．
【解】：
20．(10分) 任意给定3个正数，设计一个算法判断分别以3个数为三边的三角形是否存在，画出算法流程图．
【解】：
21．(10分)下面是一个无序列数据列：{172,35,19,288,231,343,56,16,85,513)，用冒泡排
序法将其由大到小排列成一个有序列，试画出它的算法流程图，其中赋初值R[1]：=172，R[2]：=35，…，R[10]：=513．
【解】：
20．(10分) 写出用二分法求方程
在[1，2]内的一个近似解(精确度为0．1)的一个算法，并用循环语句描述这个算法．
【解】：
答 案
三、 选择题：
2、 C 2、D 3、B 4、D 5、A 6、C 7、A 8、B 9、A 10、C 11.B 12.C
四、 填空题：
13、6 14、x：= -10；y：=
15、43 16、4
三、解答题：
17、（1）输入x1，y1，x2，y2；（2）d：＝
；
（3）输出d；（4）结束
18、算法步骤：（1）判断a是否为0，如果a为0，则判断b是否为0，是输出“x有无穷多解”，否则输出“无解”
（2）如果a不为0，则计算并输出“x＝
”
19、算法步骤：（1）判断x≥0是否成立
（2）是，计算3x，并输出；
（3）否，计算－x＋3，并输出
（4）结束
20、算法步骤：
21、略
22、算法步骤：
2004学年第二学期
高中数学必修3第三章(概率)检测题
班级 姓名 学号
一、选择题：（本题共10小题，每小题3分，共30分，在每小题给出的四个选项中，只有一项是符合题目要求的）
1．下列说法正确的是( )．
A．如果一事件发生的概率为十万分之一，说明此事件不可能发生
B．如果一事件不是不可能事件，说明此事件是必然事件
C．概率的大小与不确定事件有关
D．如果一事件发生的概率为99.999％，说明此事件必然发生
2．从一个不透明的口袋中摸出红球的概率为1/5，已知袋中红球有3个，则袋中共有除颜色外完全相同的球的个数为( )．
A．5个 B．8个 C．10个 D．15个
3．下列事件为确定事件的有( )．
(1)在一标准大气压下，20℃的纯水结冰
(2)平时的百分制考试中，小白的考试成绩为105分
(3)抛一枚硬币，落下后正面朝上
(4)边长为a，b的长方形面积为ab
A．1个 B．2个 C．3个 D．4个
4．从装有除颜色外完全相同的2个红球和2个白球的口袋内任取2个球，那么互斥而不对立的两个事件是( )．
A．至少有1个白球，都是白球 B．至少有1个白球，至少有1个红球
C．恰有1个白球，恰有2个白球 D．至少有1个白球，都是红球
5．从数字1，2，3，4，5中任取三个数字，组成没有重复数字的三位数，则这个三位数大于400的概率是( )．
A．2/5 B、2/3 C．2/7 D．3/4
6．从一副扑克牌(54张)中抽取一张牌，抽到牌“K”的概率是( )．
A．1/54 B．1/27 C．1/18 D．2/27
7．同时掷两枚骰子，所得点数之和为5的概率为( )．
A．1/4 B．1/9 C．1/6 D．1/12
8．在所有的两位数(10~99)中，任取一个数，则这个数能被2或3整除的概率是( )．
A．5/6 B．4/5 C．2/3 D．1/2
9．甲、乙两人下棋，甲获胜的概率为40％，甲不输的概率为90％，则甲、乙两人下成和棋的概率为( )．
A．60％ B．30％ C．10％ D．50％
10．根据多年气象统计资料，某地6月1日下雨的概率为0.45，阴天的概率为0.20，则该日晴天的概率为( )．
A．0.65 B．0.55 C．0.35 D．0.75
二、填空题：（本题共4小题，共18分，请把答案填写在答题纸上）
11.（3分）对于①“一定发生的”，②“很可能发生的”，③“可能发生的”，④“不可能发生的”，⑤“不太可能发生的”这5种生活现象，发生的概率由小到大排列为(填序号) 。
12．（6分）在10000张有奖明信片中，设有一等奖5个，二等奖10个，三等奖l00个，从中随意买l张．
(1)P(获一等奖)= ，P(获二等奖)= ，P(获三等奖)= ．
(2)P(中奖)= ，P(不中奖)= ．
13．（3分）同时抛掷两枚骰子，则至少有一个5点或6点的概率是 ．
14．（6分）下表为初三某班被录取高一级学校的统计表：
|
| 重点中学 | 普通中学 | 其他学校 | 合计 |
| 男生/人 | 18 | 7 | 1 | |
| 女生/人 | 16 | 10 | 2 | |
| 合计/人 |
(1)完成表格．
(2)P(录取重点中学的学生)= ； P(录取普通中学的学生)= ；
P(录取的女生)= ．
三、解答题：（本题共6小题，共52分，解答应写出文字说明，证明过程或演算步骤.）
15．(8分) 由经验得知，在某商场付款处排队等候付款的人数及概率如下表：
| 排队人数 | 0 | 1 | 2 | 3 | 4 | 5人以上 |
| 概率 | 0.1 | 0.16 | 0.3 | 0.3 | 0.1 | 0.04 |
(1)至多有2人排队的概率是多少? (2)至少有2人排队的概率是多少?
【解】：
16．(10分) 2．袋中有除颜色外完全相同的红、黄、白三种颜色的球各一个，从中每次任取1个．有放回地抽取3次，求：
(1)3个全是红球的概率． (2)3个颜色全相同的概率．
(3)3个颜色不全相同的概率． (4)3个颜色全不相同的概率．
【解】：
17．(8分) 某地区的年降水量在下列范围内的概率如下表所示：
| 年降水量／mm | [100，150) | [150，200) | [200，250) | [250，300) |
| 概率 | 0.12 | 0.25 | 0.16 | 0.14 |
(1)求年降水量在[100，200)(mm)范围内的概率；
(2)求年降水量在[150，300)(mm)范围内的概率．
【解】：
18．(8分) 抛掷一均匀的正方体玩具(各面分别标有数1，2，3，4，5，6)，若事件A为“朝上一面的数是奇数”，事件B“朝上一面的数不超过3”，求P(A+B)．
下面的解法是否正确?为什么?若不正确给出正确的解法．
解 因为P(A+B)＝P(A)+P(B)，而P(A)＝3/6=1/2，P(B)＝3/6=1/2，
所以P(A+B)＝1/2+1/2=1．
【解】：
19．(15分) 一年按365天计算，两名学生的生日相同的概率是多少?
【解】：
20．(10分) 抽签口试，共有10张不同的考签．每个考生抽1张考签，抽过的考签不再放回．考生王某会答其中3张，他是第5个抽签者，求王某抽到会答考签的概率．
【解】：
答 案
五、 选择题：
3、 C 2、D 3、C 4、C 5、A 6、D 7、B 8、C 9、D 10、C
六、 填空题：
11、④⑤③②①
12、（1）
；
；
（2）
；
13、
14、（1）略 （2）
；
；
三、解答题：
15、（1）0.56 （2）0.74
16、（1）
；（2）
；（3）
；（4）
17、（1）0.37 （2）0.55
18、
19、
20、
（等可能事件，与抽签顺序无关）