|
2005－2006学年度上学期
高中学生学科素质训练
高一数学同步测试（2）—含绝对值的不等式解法与一元二次不等式解法
说明：本试卷分第I卷和第II卷两部分，第I卷60分，第II卷90分，共150分；答题时间150分钟．
第Ⅰ卷（共60分）
一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的．
1．设集合P={1，2，3，4}，Q={
}，则P∩Q等于
（ ）
A．{1，2} B．{3，4} C．{1} D．{-2，-1，0，1，2}
2． 下列一元二次不等式中, 解集为Æ的是 （ ）
A．(x-3)(1-x)<0 B． x2-2x+3<0 C．(x+4)(x-1)<0 D．2x2-3x-2>0
3．若不等式ax2+8ax+21<0的解集是{x-7<x<-1}那么a的值是 （ ）
A．1 B．2 C．3 D．4
4．已知不等式x2-2x-3<0的解集为A, 不等式x2+x-6<0的解集是B, 不等式x2+ax+b<0的解
集是AÇB, 那么a+b等于 （ ）
A．-3 B．1 C．-1 D． 3
5．已知集合
，则集合
= （ ）A．{
} B．{
}
C．{
} D． {
}
6．已知集合A={xx－1＜2}，B={xx－1＞1}，则A∩B等于 （ ）
A．{x－1＜x＜3} B．{xx＜0或x＞3}
C．{x－1＜x＜0} D．{x－1＜x＜0或2＜x＜3}
7．不等式
的解集是 （ ）
A．
B．
C．
D．
8．不等式
的解集是 （ ）
A．（-1，3） B．（-3，1）
（3，7）
C．（-7，-3） D．（-7，-3）（-1，3）
9．己知关于x的方程(m＋3)x2－4mx＋2m－1=0的两根异号，且负根的绝对值比正根大，那么实数m的取值范围是 （ ）
A．－3＜m＜0 B．m＜－3或m＞0 C．0＜m＜3 D．m＜0 或 m＞3
10．设⊙O1、⊙O2的半径分别为r1,r2,d=O1O2、, ⊙O1和⊙O2相交的充要条件是 （ ）
A．d<r1+r2 B．d
C．
D．d<r1+r2或d>
11．已知集合A={
} B={
}则A
= （ ）
A．R B．{
}
C．{
} D．{
}
12． 设集合
,则能使P∩Q=
成立的
的值是（ ）
A．
B．
C．
D．
第Ⅱ卷（共90分）
二、填空题：本题共4小题，每小题4分，共16分．把答案填在题中的横线上．
13．已知集合M=
，N=
，那么M
N=__________．
14．不等式ax2+bx+c>0的解集为{xx<-1,或x>2}, 那么不等式ax2-bx+c>0的解集是_________．
15．若不等式
<６的解集为（－１，２），则实数ａ的值为_______．
16．设
为正整数, 则不等式
的解集是
．
三、解答题:本大题共6小题，共74分．解答应写出必要的文字说明、证明过程及演算步骤．
17．若不等式mx2+(2m+1)x+9m+4<0的解集为R, 求实数m的取值范围．(12分)
18．解关于x的不等式x2-(a+a2)x+a3>0． (12分)
19．解关于x的不等式
(12分)
20．已知集合A={a
关于x的方程x2-ax+1=0,有实根}，B={a不等式ax2-x+1>0对一切x
R成立},求A
B．(12分)
21．已知二次函数y＝x2＋px＋q，当y＜0时，有－
＜x＜
，解关于x的不等式
qx2＋px＋1＞0． (12分)
22．m是何值时, 不等式(m+1)x2-2(m-1)x+3(m-1) ≥0 (m ¹ -1)对于任何xÎR都成立? (1４分)
|
2005－2006学年度上学期
高中学生学科素质训练
高一数学同步测试（2）—含绝对值的不等式解法与一元二次不等式解法答案
一、选择题
1．A 2．B 3．C 4．A 5．C 6．D 7．A 8．D 9．A 10．C 11．B 12．B
二、填空题
13．
．14．{xx>1或x<-2}．
15．－４． 16．
．
三、解答题
17．分类讨论：①当m=0时, 原不等式变为2x+4<0, 显然它的解集不是R,所以m=0不满足条件
②当m¹0时,
只要满足 D=[2(m+1)]2-4m(9m+4)<0，且m<0即可,
解得m<-
．由①②知, m<-
18．原不等式变形(x-a)(x-a2)>0．
① 当a>1或a<0时, 有a2>a, 故原不等式解集为{xx>a2或x<a}；
② 当0<a<1时, 有a2<a, 故原不等式解集为{xx>a或x<a2}；
③ 当a=0或a=1时, 有a2=a, 故原不等式解集为{xx¹a}．
19．由
当
时，解集是R；当
时，解集是
．
20．{a
}．
21．由不等式
的解集为
，得
2和4是方程
的两个实数根，且
．(如图)
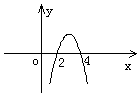
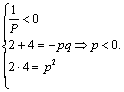
解得
说明：也可从
展开，比较系数可得．
22．因m¹-1且(m+1)x2-2(m-1)x+3(m-1) ≥0对于任何xÎR都成立, 则只要满足
D=[-2(m-1)]2-4(m+1)´3(m-1) ≤0且m+1>0即可，
解这个不等式，得 m≥2．
所以, 当m≥2 时, 不等式(m+1)x2-2(m-1)x+3(m-1)≥0(m¹-1) 对于任何xÎR都成立．