高一数学测试卷2(基本初等函数、函数的应用)
班级: 姓名: 学号:
一、 选择题:(4分×10=40分)
1、函数![]() 的定义域为( )
的定义域为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
2、当![]() >1时,在同一坐标系中,
>1时,在同一坐标系中,![]() 与
与![]() 的图像大致是( )
的图像大致是( )
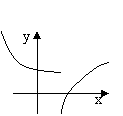
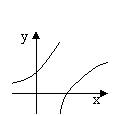
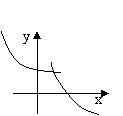
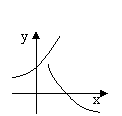
A B C D
3、已知![]() ,那么
,那么![]() 的值为( )
的值为( )
A、16 B、4 C、14 D、18
4、若![]() 是任意实数,且有
是任意实数,且有![]() ,则下列结论恒成立的是( )
,则下列结论恒成立的是( )
A、![]() B、
B、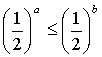 C、
C、![]() D、
D、![]()
5、下列函数中随![]() 的增大,增长率最终最大的是( )
的增大,增长率最终最大的是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
6、一批设备价值![]() 万元,由于使用磨损,每年比上一年价值降低b%,n年后这批设备的价值为 ( )
万元,由于使用磨损,每年比上一年价值降低b%,n年后这批设备的价值为 ( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
7、函数![]() 的反函数的图像经过点( )
的反函数的图像经过点( )
A、(1,2) B、(1,0) C、(2,3) D、(3,2)
8、若0<![]() <1,在区间(0,1)上,函数
<1,在区间(0,1)上,函数![]() 是( )
是( )
A、增函数且![]() <0
B、减函数且
<0
B、减函数且![]() <0
<0
C、增函数且![]() >0
D、减函数且
>0
D、减函数且![]() >0
>0
9、向高为H的水瓶中注水,注满为止,如果注水量V与水深h的函数关系的图像如图所示,那么水瓶的形状是( )




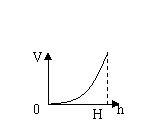
A B C D
10、函数 ,若
,若![]() ,则
,则![]() 的个数为( )
的个数为( )
A、1个 B、2个 C、3个 D、4个
| 选择题 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二、 填空题:(4分×4=16分)
11、所有指数函数的图像都通过点 ,所有对数函数的图像都通过点 ,所有幂函数的图像都通过点 。
12、已知![]() ,则
,则![]() =
=
13、若函数![]() 在区间
在区间![]() 上有一个零点。(
上有一个零点。(![]() 是整数,且
是整数,且![]() ),则
),则![]()
14、函数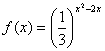 的单调递增区间为
的单调递增区间为
三、 解答题:(共44分)
15、已知:![]() ,求(1)
,求(1)![]() ;(2)
;(2)![]() .(8分)
.(8分)
16、若实数![]() 满足
满足![]() <1,求
<1,求![]() 的取值范围.(8分)
的取值范围.(8分)
17、已知函数![]() ,
,
(1)判断函数的奇偶性; (2)证明:![]() 在
在![]() 上是增函数.(10分)
上是增函数.(10分)
18、设![]() 时,求
时,求![]() 的值域.(8分)
的值域.(8分)
19、某商店进货单价为45元,若按50元一个销售,能卖出50个;若销售单价每涨1元,销售量就减少2个。设所获利润为![]() ,销售单价为
,销售单价为![]() ,
,
(1)销售单价为55元时,求所获利润为多少元?
(2)请写出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)为了获得最大利润,此商品的最佳售价应为多少元?(10分)