2005学年第一学期
杭州二中高一年级期终考试数学试卷
命题 杨 帆 校对 张先军
一、选择题
1．等差数列
的第15项为（ ）
（A）40 （B）53 （C）63 （D）76
2．若集合
，则
=（ ）
（A）
（B）
（C）
（D）
3．“
”是“
成等比数列”的（ ）
（A）充分不必要条件 （B）必要不充分条件
（C）充要条件 （D）既非充分又非必要条件
4．在数列
中，
，则此数列前四项之和为（ ）
（A）－2 （B）2 （C）1 （D）0
5．函数
的反函数为（
）
（A）
（B）
（C）
（D）
6．在各项均为正数的等比数列中，首项
，前三项和为21，则
的值为（
）
（A）33 （B）72 （C）84 （D）189
7．函数
的递减区间是（
）
（A）
（B）
（C）
（D）
8．设等差数列的前
项和为
，若
，则
的值为（
）
（A）60 （B）45 （C）36 （D）18
9．若方程
有三个根，则
的值为（ ）
（A）－2 （B）
（C）－2或 （D）不存在
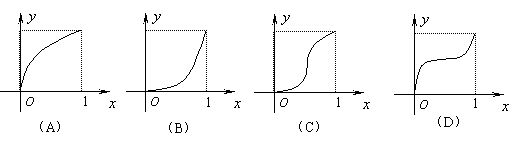10．给定的函数
，其图象在下列图中，并且对任意
，由关系式
得到的数列满足
，则该函数的图象是（
）
二、填空题
11．化简
=_________________；
12．数列
的前项和为______．
13．如图是小明同学用火柴搭的1条、2条、3条“金鱼”
搭1条“金鱼”要用8根火柴，则搭100条“金鱼”需要火柴_______________根．
14．已知
是定义在
上的不恒为零的函数，且对于任意的
，满足
．又已知
，考查下列结论：①
；②
；③
是
的等比中项；④
是
的等差中项．其中正确的是_____________．（填上所有正确命题的序号）
2005学年第一学期
杭州二中高一年级期终考试数学答卷
命题 杨 帆 校对 张先军
一、选择题（本大题共10小题，每小题4分，总计40分）
|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
题号二、填空题（本大题共4小题，每小题4分，总计16分）
11．_________； 12．________________； 13．_________； 14．___________．
三、解答题（本大题共5小题，共44分）
15．（本小题满分8分）试求函数
的定义域和值域．
16．（本小题满分8分）已知数列的前项和
（
），求数列
的前项和
．
17．（本小题满分8分）已知二次函数
．
（Ⅰ）若函数在区间
上单调递增，试求的取值范围；
（Ⅱ）若不等式
在
上恒成立，试求的取值范围．
18．（本小题满分8分）某企业投资1千万元于一个高科技项目，每年可获利
，由于企业间竞争激烈，每年年底需要从利润中取出资金200万元进行技术改造与广告投入，其余资金全部投入再生产方能保持原有的利润增长率．问经过多少年，该项目的资金（扣除最后一年的技术改造与广告投入资金）可以达到或超过翻两番的目的？（
）
19．（本小题满分12分）已知
，数列是首项为
，公差为
的等差数列；
是首项为
，公比为
的等比数列，且满足
．
（Ⅰ）求数列和的通项公式；
（Ⅱ）若存在
，试求数列
的前项和；
（Ⅲ）是否存在数列
，使得
对一切大于1的正整数都成立，
若存在，求出；若不存在，请说明理由．
四、附加题（本题满分4分，计入总分，但卷面分不超过100分）
20．观察下列数表，问此表最后一个数是什么，并说明理由．
 |
2005学年第一学期杭州二中高一期终试卷数学（参考答案）
一、选择题（本大题共10小题，每小题4分，总计40分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | B | A | D | D | A | C | A | B | C | B |
二、填空题（本大题共4小题，每小题4分，总计16分）
11． 6 ； 12．
； 13． 602 ； 14． ①③④ ．
三、解答题（本大题共5小题，共44分）
15．（本小题满分8分）试求函数的定义域和值域．
〖解答〗
（1）由
，故定义域为
；
（2）解法1：由
，故值域为
解法2：设
则
，由
，
进一步可得值域为．
16．（本小题满分8分）已知数列的前项和，求数列的前项和．
〖解答〗当
时，
，当
时，
，
综上可得：
．又由通项公式可知当
时
，因此有
当
时，
；
当时，
．
综上可得：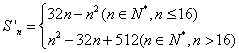
17．（本小题满分8分）已知二次函数．
（Ⅰ）若函数在区间上单调递增，试求的取值范围；
（Ⅱ）若不等式在上恒成立，试求的取值范围．
〖解答〗由于
，（1）由题意可得
．
（2）解法1：由题意得
在上恒成立，即
在上恒成立．令
，由其图象可知
在上的最小值为
（当
时取到），故
．
解法2：
在上恒成立，
当
时
；当
时
；当
时
，此时无解，综上可得．
18．（本小题满分8分）某企业投资1千万元于一个高科技项目，每年可获利，由于企业间竞争激烈，每年年底需要从利润中取出资金200万元进行技术改造与广告投入，其余资金全部投入再生产方能保持原有的利润增长率．问经过多少年，该项目的资金（扣除最后一年的技术改造与广告投入资金）可以达到或超过翻两番的目的？（）
〖解答〗设第年终资金为
万元，由题意可得
，变形整理可得：
，故
构成一个等比数列，
，
，故
，
令
，得
，两边取对数可得：
，
故至少要12年才能达到目标。
解法2：此题在求通项公式时，也可采用迭代法，如下：
=
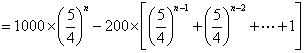
19．（本小题满分12分）已知，数列是首项为，公差为的等差数列；是首项为，公比为
的等比数列，且满足
．
（Ⅰ）求数列和的通项公式；
（Ⅱ）若存在，试求数列的前项和；
（Ⅲ）是否存在数列，使得对一切大于1的正整数都成立，
若存在，求出；若不存在，请说明理由．
〖解答〗
（Ⅰ）
；
．
（Ⅱ）由错位相减法，可得
（Ⅲ）假设存在满足条件的数列，则有
，且有
解法1：
，两边同除以
可得
，
令
，则有
，故
是首项为－1，公差为
的等差数列，则
，故
．
解法2：由迭代法可得
四、附加题（本题满分4分，计入总分，但卷面分不超过100分）
20．观察下列数表，问此表最后一个数是什么，并说明理由．
|
〖解答〗
方法（一）：各行首末项之和为：101、202、404、808组成等比数列．故
．
方法（二）：各行第一个数依次为：
，
，
，
故
．
方法（三）：第行各数之和为
，其中
为项数，当
，即
时，
为最后一个数．
方法（四）：若记第
行的第个数为
，则有
，
，令
，而
，故
，
当时，
，即此表最后一个数是．