红岭中学高一年级立体几何单元测试(2004.12.15)

（时间：45分钟　 满分：100分）

学号：　　　　  班级：　　　 姓名：

一、选择题：（本大题共10小题，每小题5分，共50分）

1、若两条直线与第三条直线都垂直，则这两条直线的位置关系是　　　　（　　 ）

A．平行　　B. 相交　　C　异面　　  D 以上都有可能

2、点M在直线a上，直线a在平面α内，可用符号记为　　　　　　  （　　　 ）

A、M∈a, a∈α　　　　  　　 B、M∈a, aα

C、Mα, aα　　　　　  D、Mα, a∈α

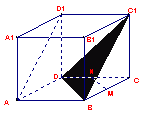
3、右图的正方体中，M、N是棱BC、CD的中点，

则异面直线AD₁与MN所成的角为　　　　  （　　 ）度

A. 30　　　　　　 B　45　　

C 60　　　　　　 D　90

4、点P在平面ABC外，若PA=PB=PC，则点P在平面ABC上的射影

是△ABC的　　　　　　　　　　　　　　　　　　　　　　　　　 （　　　 ）

（A）外心　　（B）重心　　（C）内心　　  （D）垂心

5、长、宽、高分别为4、3、的长方体的外接球的体积为　　　　 （　　　 ）

 （A）3　　 （B）　 　 （C） 　　（D）9

6、设α、β、γ为平面，a、b为直线，则能推出α∥β的一个条件是　　（　　　）

（A）α⊥γ且β⊥γ　　　 （B）a∥α且a∥β

（C）a⊥α且a⊥β　　　 （D）α∩γ=a，β∩γ=b且a∥b

7、右图所示的直观图，其平面图形的面积是（　　  ）

A．4　　　 B. 4　　 C. 2　　D. 8　

8、已知两条直线a、b及平面α有四个命题：

①若a∥b且a∥α则b∥α;　②若a⊥α且b⊥α则a∥b;

③若a⊥α且a⊥b则b∥α; ④若a∥α且a⊥b则b⊥α;　 其中正确的命题是(　　  )

  A　①　　　 B②　 C　③　　　 D ④

9、在30°的二面角a-l-b中，P∈a，PQ⊥b，垂足为Q，PQ=2a，

则点Q到平面a的距离为　　　　　　　　　　　　　　　　　　　　　　 （　　　 ）

（A）a　　（B）a　　（C）a　（D）a

10、长方体ABCD—A₁B₁C₁D₁中，AB=2，BC=3，AA₁=5，则一只小虫从A点沿长方体的表面爬到C₁点的最短距离是　　　　　　　　　 　　　　　　　　　　 （　　　）

A 　B 5　 C 17　 D 3+

二、填空题（5¢´4=20¢）

11、二面角的平面角的取值范围是　　　　　　　　　　

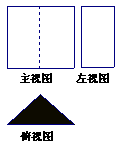
12、右图的三视图表示的几何体是　　　　　 

13、底面直径和高都是4cm的圆柱的侧面积为_________cm²

14、如图，Rt△ABC中，∠ACB=90º，∠BAC=45º，

PA⊥平面ABC，且PA=BC=1，

则二面角A—PB—C的平面角的是　　　　 

 

 

 

三、解答题（30¢）

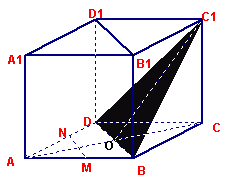
15、（满分10¢）正方体ABCD—A₁B₁C₁D₁中，M、N分别为棱AB、AD的中点，O为AC与BD的交点，求证：MN⊥OC₁

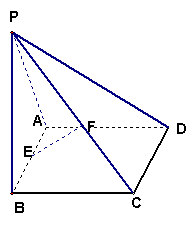
16、（满分10¢）如图，四棱锥P—ABCD底面是平行四边形，E、F分别是AB和PC的中点，求证：EF∥平面PAD

　

17、（满分10¢）已知正四棱锥的底面边长为6cm，体积是36cm³.（1）求侧面与底面所成角；（2）求此棱锥的全面积.

答案：DBCAB　CABAB

0⁰≤θ≤180⁰　三棱柱　 16π　　60⁰

17题：60⁰　108cm²