2006年惠州市第一中学高一数学必修3单元测试

算　法　试　题（2006年4日7日）

一、选择题：本大题共10小题，每小题4分，共40分．在每小题给出的四处备选项中，只有一项是符合题目要求的．

1．算法的三种基本结构是(　　)

　 （A）顺序结构、条件结构、循环结构　　　（B）顺序结构、循环结构、模块结构

　 （C）顺序结构、模块结构、条件结构　　　（D）模块结构、条件结构、循环结构

2．将两个数a=25，b=9交换，使a=9，b=25，下面语句正确一组是 (　　)

（A）　　　　　 （B）　　　　　 （C）　　　　　　 （D）

	a=b b=a						a = c c = b b = a
					t = b b = a a = t
			b=a a=b

3．下列各数中，最小的数是（　　 ）。

　 （A）111 111_（2） 　　 （B）105_（8） 　　 （C）200_（6） 　　 （D）75

4．下列给变量赋值的语句正确的是（　）

（A）5＝a　　　　（B）a＋2＝a　　　（C）a＝b＝4　　 （D）a＝2*a

5．下面程序运行后，a，b，c的值各等于　  （　 ）

a = 3

b = - 5

c = 8

a = b

b = c

c = a

PRINT  a, b, c

END

(A) –5,8,-5　　　　  (B) –5,8,3　　　　 (C) 8,–5,3　　  (D) 8,–5,8

6．为了在运行下面的程序之后得到输出y＝16，键盘输入x应该是（　　）。

　　　  Input x

If　x<0　then

y=(x+1)*(x+1)

Else

y=(x-1)*(x-1)

　　　　End if

Print y

End

(A) 3或-3　　　　　  (B) -5　　　　　 (C) -5或5　　　　 (D) 5或-3

7．读两段程序：

甲：i=1　　　　　　　  乙：i=1000 S=0　　　　　　　　 　 S=0 WHILE i<=1000　　　 　 DO S=S+i　　　　　　 　　 S=S+i i=i+1　　　　　　 　　 i=i-1 WEND　　　　　　　　　 LOOP UNTIL i<1 PRINT S　　　　　　 　 PRINT S END　　　　　　　　 　 END

对甲、乙程序和输出结果判断正确的是（　　 ）

（A）程序不同，结果不同　　　　　　  （B）程序不同，结果相同

（C）程序相同，结果不同　　　　　　  （D）程序相同，结果相同

8．用二分法求方程的近似根，精确度为δ，用直到型循环结构的终止条件是（　　）。

（A）x₁－x₂＞δ　 （B）x₁－x₂＜δ　 （C）x₁＜δ＜x₂　 （D）x₁=x₂=δ

9．给出下面的程序框图，那么其循环体执行的次数是　 （　 ）

(A) 500　　　　　  (B) 499　　　　　　 (C) 1000　　　　　　 (D) 998

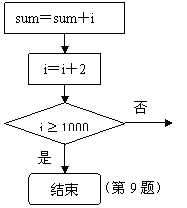
10．已知有上面程序，如果程序执行后输出的结果是11880，那么在程序UNTIL后面的“条件”应为 (　　 )

(A)  i > 9　　　　(B)　i >= 9　　　 (C)  i <= 8　　　 (D)　i < 8

姓名_______________　班别_______________　 学号__________

请将第一部分选择题答案填入下列表格内。（共10题，每小题4分，共40分。）

题号	1	2	3	4	5	6	7	8	9	10
答案

二、填空题：本大题共4小题，每小题4分，共16分．把答案填在题中相应的横线上．

11．下列四个有关算法的说法中，正确的是　 　　　　　　 . ( 要求只填写序号 )

　　(1) 算法的某些步骤可以不明确或有歧义，以便使算法能解决更多问题；

　　(2) 正确的算法执行后一定得到确定的结果；

　　(3) 解决某类问题的算法不一定是唯一的；

　　(4) 正确的算法一定能在有限步之内结束。

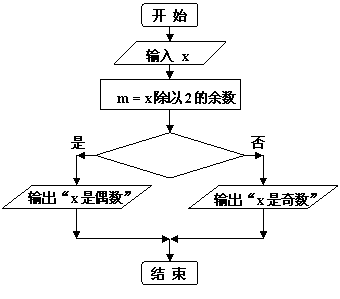
12．右边的程序框图（如图所示），

能判断任意输入的整数x是奇数

或是偶数。其中判断框内的条件

是________________。

程序2如下： i = 51 sum = 0 do　 　　 sum=sum＋i 　　　 i = i＋1 loop　until  i > 50 print　sum end

程序1如下： i = 51 sum = 0 while　i <= 50 　　 sum=sum＋i 　　　 i = i＋1 wend print　sum end

13．已知有如下两段QBasic程序：

问：程序1运行的结果为_______________。　 程序2运行的结果为_______________。

14．把下面求n！（ n!= n×(n-1)×……×3×2×1 ）的程序补充完整

	________________“n＝”；n i＝1 s＝1 WHILE _______________ _________________ i = i+1 WEND PRINT　s END

三、解答题：本大题共4小题，共44分．解答应写出文字说明、演算步骤或推证过程。

15．(本题满分8分)

用秦九韶算法计算函数时的函数值。

16．(本题满分12分)

已知算法：（1）指出其功能（用算式表示），

（2）将该算法用流程图描述之。

17．(本题满分12分)

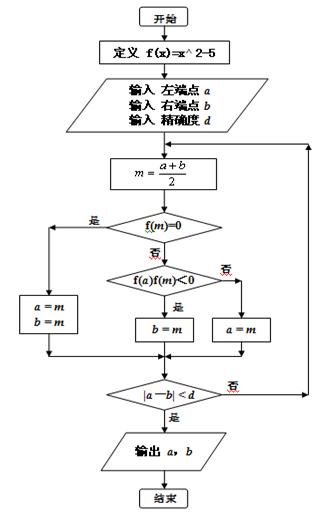
以下程序流程图及其相应程序是实现用二分法求近似值，但步骤并没有全部给出，请补上适当的语句或条件，以保证该程序能顺利运行并达到预期的目的。

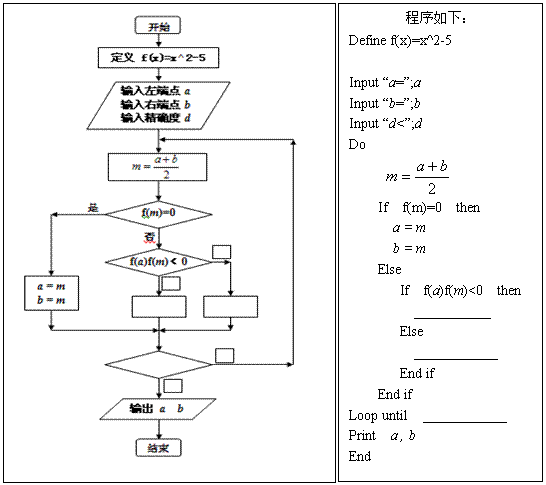
18．(本题满分12分)

已知S=1²－2²＋3²－4²＋……＋(n－1)²－n²，

请设计程序框图，算法要求从键盘输入n，输出S。并写出计算机程序。

四、附加题 (本题满分20分)

　 某大型超市在嘉年华推出购物优惠活动，规则如下：

当购物件数 n < 5 时，总金额按商品的原价收取。

当购物件数 5 =< n < 10时，赠送其中价格最低的一件商品，但赠送的商品价格超过10000元的只赠送10000元。

当购物件数 n >= 10 时，所有商品七折优惠。

为了配合超市的活动，公司要更新收银系统的软件。软件算法要求是：

输入购买商品的件数和各件商品的价格，输出收银员优惠后应收取的总金额。

现在请你为这个软件系统的算法设计一个程序框图。

算法试题答案

A C A D A　　C B B B C

11．（2）（3）（4）　　　　 12．m=0 ?　　　

13．0 ，51　　　　　　　 14．Input ，　i<=n，　s=s*i

三、解答题

15．解：f(x)=2x ⁴+3x ³+5x－4

　　　　　 =x (2x ³+3x ²+5)－4

　　　　　 = x[x² (2x +3 )+5]－4

∴f(x)= 2[2² (2*2+3 )+5]－4

　　 = 2[4*7+5]－4

　　 =2*33－4

　　 =62

16．解：算法的功能为：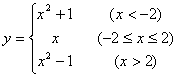

y = x

y = x 2+1

y = x 2－1

否

是

否

是

x < 2　？

x < －2　？

结束

输出 y

输入 x

开始

　　　　程序框图为：

17．

			程序如下： Define f(x)=x^2-5 Input “a=”；a Input “b=”；b Input “d<”；d Do 　　 If　f(m)=0　then 　a = m 　b = m Else 　 If　f(a)f(m)<0　then 　　 ___b = m____ 　 Else 　　 ___ a = m ___ 　 End if End if Loop until _abs(a－b) < d_ Print　a , b End

18．解：由表达式规律可知，输入的n必须为偶数。

　　 程序框图为：

注：程序框图也可以不对n进行奇数和偶数的讨论，直接进入循环。

四、附加题：

结束

输出 S