汕头市龙湖区新溪一中

2005-2006年度高一数学第一学期期末考试试卷

适用版本：人教新课标

一、选择题（每小题5分，共50分）

1．已知全集，集合，，那么=　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　　）

A． 　 B．　　 C．　　  D．

2．如图所示，三视图表示的几何体是　　　　　　　　　　　　　 （  　　）

正视图　　　　 侧视图　 　　　俯视图

A．棱锥；　　　B．圆柱；　　　C．圆锥；　　　D．圆台；

L3

3．若图中的直线L₁、L₂、L₃的斜率分别为K₁、K₂、K₃则　　　　 （　　　）

L2

　　　　  A．K₁﹤K₂﹤K₃

B．K₂﹤K₁﹤K₃

o

x

　　　　  C．K₃﹤K₂﹤K₁

L1

　　D．K₁﹤K₃﹤K₂

　　　　　　　　　 

4．直线3x+4y-13=0与圆的位置关系是：　　　　 （　　　）

A. 相离　　 B. 相交　　 C. 相切　　 D. 无法判定.

5．如果函数在区间上是减函数，那么实数的取

值范围是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　  （　 　）

A．　　　　 B．　　　　　 C．　　　　　 D．

6．三个数，，的大小顺序是　　　　　　　　　　　　 (　　　)

A．　　B．　

C．　　D．

7．设a，b是两条不同的直线，是两个不同的平面，则下列四个命题：(　　 )

1若；　　　　2若；

3若；　　　 4若；

其中正确的命题的个数是　　　　　　　　　　　　　　　　　　　  （　　 ）

A．0个；　　　　B．1个；　　　 C．2个；　　　 D．3个；

8．如果直线ax＋y＋1=0与直线3x－y－2=0垂直，那么系数a为　　 (　　 )

　 A．－3　　　　B．3　　　　　 C．　　　　　 D．

9．设,用二分法求方程 内近似解的过程中得则方程的根落在区间　　　　　　 (　　 )

A．（1，1.25）　　　 B．（1.25，1.5）　　　

C．（1.5，2）　　　　D．不能确定

10． 如图，在正四棱柱ABCD－中(底面是正方形的直棱柱)，侧棱=， ，则二面角的大小为　　　　　　　　　  (　　)　　　

A．30^o　　　 B．45^o　　　　C．60^o　　　 D．90^o

二、填空题（每小题5分，共20分）

11．函数的定义域为了 ______．

12．一个正方体的顶点都在球面上，它的棱长为1cm，则球的体积为　 __．

13．自点A（－1，4）作圆(x－2)²+(y－3)²=1的切线m，则切线m的方程为 ____.

14．直线x－2y－3=0与圆(交于E、F两点，则△EOF(O为坐标原点）的面积等于　　　　.

 

三、解答题(本大题共6个小题，共80分。解答题应写出文字说明、证明过程或演算步骤。)

15．（12分）已知函数

(1)用定义证明是偶函数；　　　(2)用定义证明在上是增函数

 

16．(12分) 已知三角形ABC的顶点坐标为A（－1，5）、B（－2，－1）、

C（4，3），M是BC边上的中点。

(1) 求中线AM所在的直线方程；(2) 求AC边上的高所在的直线方程。

17．（14分）已知关于x,y的方程C:.

(1)当m为何值时，方程C表示圆。

(2)若圆C与直线：相交于M,N两点，且MN=,求m的值。

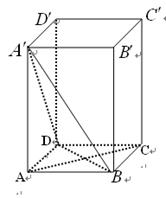
18．(14分)如图，在棱长为1的正方体中：

（1）　　求异面直线与所成的角的大小；

（2）　　求三棱锥的体积；

（3）　　求证：。

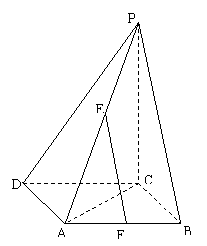19．(14分)如图，在边长为a的菱形ABCD中，，E，F是PA和AB的中点。

（1）求证： EF∥平面PBC _;

（2）求E到平面PBC的距离。

 

20．（14分）医学上为了研究传染病在传播的过程中病毒细胞的生长规律及其预防措施，将一种病毒细胞的m个细胞注入一只小白鼠的体内进行试验。在试验过程中，得到病毒细胞的数量与时间的关系记录如下表：

时间（小时）	1	2	3	4	5	6	7
病毒细胞总数（个）	m	2m	4m	8m	16m	32m	64m

　 已知该种病毒细胞在小白鼠体内超过m个时，小白鼠将死亡，但有一种药物对杀死此种病毒有一定效果，用药后，即可杀死其体内的大部分病毒细胞。

（1）在16小时内，写出病毒细胞的总数与时间的函数关系式。

(2)为了使小白鼠在实验过程中不死亡，最迟应在何时注射该种药物。（精确到小时，）

2005-2006年度高一数学期末考试参考答案

一、选择题

1	2	3	4	5	6	7	8	9	10
B	C	A	C	A	C	B	C	B	C

　　　　　　　

二、填空题

11．　 　 12．　　　　 13．　　　　　　14．　　　　　　

三、解答题

15．

（1）证明：∵

∴函数是偶函数

（2）证明：设

∵，

∴

又∵，∴＜0，>0，<0

∴<0 即

所以在上是增函数。

16．

解：（1）∵M是BC边上的中点，

B点的坐标为（－2，－1）、C点的坐标为（4，3）

∴M点的坐标为（1，1）.

由两点式写方程得 ，

即

（2）直线AC的斜率为，所以AC边上的高所在直线的斜率为 ，

又因为AC边上的高所在直线过点B（-2，-1），由点斜式方程得

，即

17.

解：（1）方程C可化为　

　　　　显然　时方程C表示圆。

（2）圆的方程化为　

　　 圆心 C（1，2），半径　

　　 则圆心C（1，2）到直线：x+2y-4=0的距离为

　　

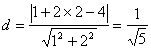
，有

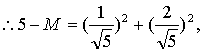得　

18．

（1）解：∵AA₁∥BB₁，

∴异面直线BC₁与AA₁所成的角就是BC₁与BB₁所成的角，即∠B₁BC₁=45^o，

故异面直线BC₁与AA₁所成的角为45^o

（2）解：

（3） 证明：如图，连结BD、B₁D₁ ，

∵A₁B₁C₁D₁是正方形，

∴A₁C₁⊥B₁D₁，

又∵BB₁⊥底面A₁B₁C₁D₁，A₁C₁底面A₁B₁C₁D₁，

∴A₁C₁⊥BB₁，

∴A₁C₁⊥平面BB₁D₁D，

∴B₁D⊥A₁C₁，同理可证：B₁D⊥BC₁，且A₁C₁∩BC₁= C₁

故B₁D⊥平面A₁C₁B

19.

（1）证明：∴EF∥PB

　　　　  又

　　　　  故

（2）解：在面ABCD内作过F作

　　　　

　　　　又 ，，

　　　　

又，故点E到平面PBC的距离等于点F到平面PBC的距离FH。

　　　在直角三角形FBH中，，

　　　

故点E到平面PBC的距离等于点F到平面PBC的距离，

等于。

20.

（1）第1小时的病毒细胞总数为个，第2小时的病毒细胞总数为个，

第3小时的病毒细胞总数为个，第4小时的病毒细胞总数为个，

……………………第小时的病毒细胞总数为个，

故。又，

所以函数的解析式为：

（2）设最迟在第小时注射药物，由（1）可得：

为了使小白鼠不死亡，应有：

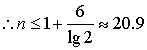
答：最迟在注入病毒细胞后的第20小时应注射药物。