2004~2005学年度高一第一学期中段考
数学试卷
说明：（1）本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分，考试时间120分钟。
（2）把各题的正确答案写到答题卡上，交卷时只需交答题卡。
第Ⅰ卷（选择题共60分）
一、选择题：（本题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）
1、若3x-1=27，则x=（ ）
A、2
B、4
C、
D、10
2、若S=
，则
等于（ ）
A、Φ
B、
C、
D、
3、函数y=(2a+3)x在
时0<y<1,则实数a的取值范围是（ ）
A、a>0
B、a>
C、<a< -1 D、a>-1
4、二次函数
的对称轴为
，则当
时，
的值为 （ ）
A、
B、1
C、17
D、25
5、集A=
，则A
等于（ ）
A、
B、
C、
D、
6、下列四个图像中，是函数图像的是 （ ）
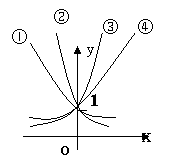
A、（1） B、（1）、（3）、（4） C、（1）、（2）、（3）D、（3）、（4）
7、如右图是指数函数①y=ax ，②y=bx，③y=cx，④y=dx的图象，
则a，b，c，d与1的大小关系是（ ）
A、a<b<1<c<d B、b<a<1<d<c
C、1<a<b<c<d D、a<b<1<d<c
8、如果函数
在区间
上是减少的，那么实数
的取值范围是（ ）
A、
B、
C、
D、
9、设
，则m＝（ ）
Ａ、
Ｂ、18 Ｃ、9 Ｄ、２７
10、已知（x,y）在映射f作用下的象是（x+y,x-y），则在f的作用下，（1，2）的象是（ ）
A、（3，-1） B、（1，2）
C、
D、
11、已知P=
，则P
等于（ ）
A、
B、
C、
D、
12、已知y=
在
上是x的减函数，则a的取值范围是（ ）
A、（0，1） B、（0，2）
C、（1，2）
D、
第Ⅱ卷（非选择题共90分）
二、填空题：（本题共4小题，每小题5分，共20分，请把答案填写在答题纸上）
13、设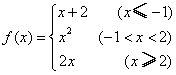
，则f(3)=
；
14、函数f(x)=
的定义域是
；
15、已知2a+2>16，且f(x)=ax ，则数f(-1)，f(1)和f(log
从小到大的次序是
；
16、设a=
，b=
，则3a+2b=
。
三、解答题：（本题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤.）
17、计算：（共12分，每小题6分）
（1）
（2）log
18、已知函数f(x)的图象与函数g(x)=ax的图象关于直线y=x对称。（1）求函数f(x)的解析式；（2）若f(
)<f(2)，试确定实数a的取值范围。（12分）
19、已知函数f(x)=
，（1）判断f(x)的奇偶性；（2）证明：函数f(x)在上
是增加的。（12分）
20、对于二次函数
，（12分）
（1）指出图像的开口方向、对称轴方程、顶点坐标；
（2）画出它的图像，并说明其图像由
的图像经过怎样平移得来；
（3）求函数在
最大值或最小值；
（4）分析函数的单调性。
21、按复利计算利息的一种储蓄，设本金为a元，每期利率为r，本利和为y，存期为x，写出本利和y随存期x变化的函数式，如果存入本金1000元，每期利率2.25%，计算5 期后的本利和是多少？（10分）
22、设函数
是定义在
上的减函数，并且满足
，
，
（1）求
的值， （2）如果
，求
的取值范围。（12分）
高一数学中段考试题答题卷
班级 姓名 学号 成绩
一、选择题答题处：（每小题5分，共60分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题答题处：（每小题5分，共20分）
13、 14、 15、 16、
三、解答题：（本题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤.）
17、计算：（共12分，每小题6分）
解：(1) (2)
18、（12分）
19、（12分）
20、（12分）
21、（10分）
22、（12分）
高一数学第一学期中考试题参考答案
一、 选择题：
BACDD BBACA DC
二、填空题：
13、6
14、
(或
)
15、f(log<f(-1)<f(1) 16、490
三、解答题：
17、（1）原式=
（2）原式=log
+log
-3
=
=2+1-3
=0
18、（1）依题意可知函数f(x)与g(x)互为反函数，故所求函数解析式为f(x)=log
。
（2）∵ f(
<f(2) ∴
log
<log
2 ∴ 0<a<1
19、解：（1）∵ f(-x)=
f(x) ∴函数f(x)=是奇函数。
（2）设
，则f(x1)-f(x2)=
∵ 
∴ 
又
∴ f(x1)-f(x2)<0 即 f(x1)<f(x2)
∴ 函数f(x)=
上是增加的。
20、（1）开口向下；对称轴为；顶点坐标为
；
（2）其图像由的图像向右平移一个单位，再向上平移一个单位得到；
（3）函数的最大值为1；最小值为-35。
（4）函数在
上是增加的，在
上是减少的。
21、解：y随x变化的函数解析式为y=a(1+r)
，（
；
5期后的本利和是1000（1+2.25%）
=1117.68元。
22、解：（1）令
，则
，∴
（2）∵ ∴
∴
，又由是定义在R＋上的减函数，得：
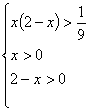解之得：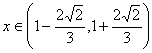
。