高一数学必修Ⅰ第一章《集合与函数概念》期末复习题
一、选择题（本题共12小题，每小题5分，共60分，每题有四个选项，其中只有一项是
正确的）
1、 设集合
，定义P※Q＝
，
则P※Q中元素的个数为 （ ）
A、3 B、4 C、7 D、12
2、满足M={a，b}
A{a,b,c,d}，A集合的个数是（ ）
A、1 B、2 C、3 D、4
3、函数y=log2(x2-2x-3)的递增区间是( )
A、(-
,-1) B、(-,1)
C、(1,+)
D、(3,+)
4、将二次函数y=
的图象向上平移一个单位，再将所得图象向左平移两个单位，
就得到函数（ ）的图象。
A、
B、
C、
D、
5、已知函数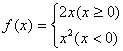
，f [f（－2
）] = ( )
A、16 B、－8 C、8 D、8或－8
6、设集合
，在下图中能表示从集合A到集合B
的映射的是（ ）
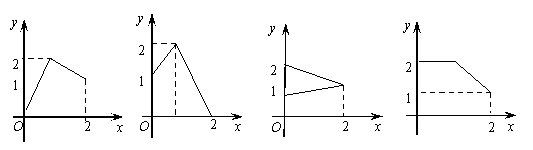
A B C D
7、函数
是奇函数，则函数
是（ ）
A、奇函数 B、偶函数 C、奇函数且偶函数 D、非奇非偶函数
8、设函数f(x)的定义域为[-1,2],则函数f(x-1)的定义域为( )
A 、[0,3] B、[-2,1] C、[-1,2] D、[0,1]
9、已知
，则
（ ）
A、6 B、7 C、8 D、9
10、若集合A={x｜kx2+4x+4=0,x∈R}只有一个元素，则实数k的值为（ ）
A、0 B、1 C、0或1 D、2
11、函数f(x)是定义在区间[-5，5]上的偶函数，且f(1)<f(3),则下列各式一定成立的
是（ ）
A、f (0) > f (5) B、f (3) < f (2) C、f (-1) > f (3) D、f (-2) > f(1)
12、设函数
+ b+ c 给出下列四个命题：
①c = 0时，y是奇函数
②b0 , c >0时，方程0 只有一个实根
③y的图象关于(0 , c)对称 ④方程0至多两个实根
其中正确的命题是 （ ）
A、①④ B、①③ C、①②③ D、①②④
二、填空题（本题共4个小题，每小题4分，共16分）
13、已知全集U={- 4，-3，-2，-1，0}，集合M={- 2，-1，0}，
N={-4，-3，0}，则
。
14、若函数f ( x )满足f ( x + 1) = x2－2x，则f ( 2 ) =
15、国家规定个人稿费纳税办法是：不超过800元的不纳税；超过800 元而不超过4000元的按超过800元部分的14%纳税；超过4000元的按全部稿酬的11%纳税。已知某人出版一本书，共纳税420元时，这个人应得稿费（扣税前）为 元。
16、函数 y = 2x2 +ax－1在( 0 , 4)上是递增的，则 a 的范围是 。
三、解答题（本题共6个小题，共74分，解答本题要求充分地展示解答过程，有必要的文字叙述，注意解题规范）
17、（10分）二次函数f（x）满足
且f（0）=1。求f（x）的解析式。
18、（12分）已知二次函数f (x) = 3x2+6x-1
(1) 把它化成f (x) = a (x + n )2 +m的形式；
(2) 求f(x)在区间[0，2]上的最值。
19、（12分）求函数
的定义域并判断奇偶性
20、（12分）已知集合A＝
，B＝
。
（1）当a＝2时，求A∩B； （2）求使BA的实数a的取值范围。
21、（13分）偶函数y= f (x)在
单调递减，解不等式f (a+2) >f (a-5)
22、(15分)某市出租车的计价标准是：4km以内 10元（含4km），超出4km且不超过18km的部分1元/km；超出18km的部分2元/km 。
（1）如果不计等待时间的费用，建立车费y与行车里程x的函数解析式，并画出函数图象；
（2）如果某人乘车行驶了20km，他要付多少车费？
（3）如果某人付出22元的车票，他坐了多远？