高一数学试题

姓名　　　　　　  　　 得分

一、　　　　　 选择题（每小题只有一个答案正确，每小题5分，共60分） 

1．已知集合M={},集合N={}，则M(　 )。

（A）{}　　　　　　　　　 （B）{}

（C）{}　　　　　　 　（D）

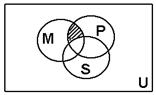
2.如图，U是全集，M、P、S是U的三个子集，则阴影部分所表示的集合是（　 ）

（A）（M　　　　　　　 （B）（M

（C）（MP）（C_US）　　　　 （D）（MP）（C_US）

3．若函数y=f(x)的定义域是[2，4]，的定义域是（　 ）

（A）[，1]　　 （B）[4，16]　　　（C）[]　　　　 （D）[2，4]

4．下列函数中，值域是R⁺的是（　 ）

（A）y=（B）y=2x+3　x)　（C）　y=x²+x+1　（D）y=

5.已知的三个内角分别是A、B、C，B=60°是A、B、C的大小成等差数列的（　 ）

（A）充分非必要条件　　　　 （B）必要非充分条件

（C）充要条件　　　　　　　 （D）既非充分也非必要条件

6．设函数f(x)满足f(x)＝f(－x)，当x时f(x)是增函数，则f(-2),f(),f(-3)的大小关系是（　 ）

（A）f()>f(-3)>f(-2)　　　　（B）f()>f(-2)>f(-3)

（C）f()<f(-3)<f(-2)　　　　（D）f()<f(-2)<f(-3)

7.a=log_0.70.8,b=log_1.10.9,C=1.1^0.9,那么（　）

（A）a<b<c　 （B）a<c<b　 （C）b<a<c　 （D）C<a<b

8.在等差数列{a_n}中，若a₂+a₆+a₁₀+a₁₄=20, 则a₈=（　 ）

（A）10　 （B）5　 （C）2．5　（D）1．25

9．在正数等比数列{a_n}中，若a₁+a₂+a₃=1,a₇+a₈+a₉=4,则此等比数列的前15项的和为（　 ）

（A）31　（B）32　（C）30　（D）33

10．设数列{a_n}的前几项和S_n=n²+n+1,则数{a_n}是（　 ）

（A）等差数列　　　　　　　　　　 （B）等比数列

（C）从第二项起是等比数列　　　　 （D）从第二项起是等差数列

11．函数y=a-的反函数是（　 ）

（A）y=(x-a)²-a　　 (xa)　　　　　　　  （B）y=(x-a)²+a　　 (xa)

（C）y=(x-a)²-a　　 (x)　　　　　　　 （D）y=(x-a)²+a　　 (x)

12．设,则 (　 )。

（A）　　  （B）　　（C）　　（D）

二、填空题（每小题4分，共16分）

13．求和　　　　　　 。

14．函数y=a^x+b(a>0且a)的图象经过点（1，7），其反函数的图象经过点（4，0），则a^b=　　　　　 

15．函数的定义域为　　　　　 

16．定义运算法则如下：

a则M+N=　　　　

 

三、解答题（本大题共74分）

17．(本小题满分12分)作出下列函数的图象，并根据图象指出函数的值域.

(1)y=; 　　　　　　　　　　　　　　　(2)y=x－x－1.

18．(本小题满分12分)求函数y=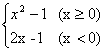的反函数

19．(本小题满分12分)已知函数y=(x∈［0,］),

(1)求它的反函数f^－1(x);

(2)判断y=f^－1(x)在其定义域上的单调性并证明.

20．.(本小题满分12分)

某桶装水经营部每天的房租、人员工资等固定成本为200元,每桶水的进价是5元.销售单价与日均销售量的关系如下表所示:

销售单价/元	6	7	8	9	10	11	12
日均销售量/桶	480	440	400	360	320	280	240

请根据以上数据作出分析,这个经营部怎样定价才能获得最大利润?（为方便收取，每桶水的定价为整数）

21．(本小题满分12分)

设有两个集合A={x},B={x},若AB=B，求a的取值范围。

22．(本小题满分14分)已知函数f(x)=ab^x的图象过点A(4,)和B(5,1).

(1)求函数f(x)的解析式.

(2)记a_n=log₂f(n),n是正整数，S_n是数列{a_n}的前n项和，解关于n的不等式a_nS_n≤0.

(3)对于(2)中的a_n与S_n，整数96是否为数列{a_nS_n}中的项？若是，则求出相应的项数；若不是，则说明理由.

高一（上）数学期末考试试题（A卷）

一、　　　　　  选择题

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案	B	C	C	D	C	A	C	B	A	D	D	A

二、填空题

13．　　　 14.　64　　15.　(0,1) 16.　5

三、解答题

17．∵ a、b、c成等差数列，∴ 2b=a+c……①。又∵a、b、c成等比数列，∴ c²=ab……②,①②联立解得a=-2c或a=-2c或a=c(舍去)，b=-,a∶b∶c=(-2c)∶(- )∶c=-4∶-1∶2。

18．（1）∵，∴ -1<x<1,即f(x)的定义域为（-1，1）。

（2）∵x(-1,1)且f(-x)=log_a为奇函数。

19．设这个摊主每天从报社买进x份报纸，每月所获的利润为y元，则由题意可知250x400,且y=0.3×x×20+0.3×250×10+0.05×(x-250) ×10-0.2×x×30=0.5x+625。

∵ 函数f(x)在[250，400]上单调递增，∴当x=400时，y最大=825，即摊主每天从报社买进400份报纸可获得最大利润，最大利润为825元。

20．A={xR}={x},B={xR}={x}

∵A,∴，解得a<,又 ∵a>,∴<a<。

21.

（1）a₁=,a₂=,a₃=,a₄=,f(1)=1-a₁=,f(2)=(1-a₁)(1-a₂)=,f(3)=(1-a₁)(1-a₂)

a₃)=,f(4)=(1-a₁)(1-a₂)(1-a₃)(1-a₄)=,故猜想f(n)=

(2)证明：①当n=1时，左式=f(1)=,右式=，∵左式=右式，∴等式成立。②假设当n=k时等式成立，即f(k)=则当n=k+1时，左式=f(k+1)=f(k)(1-a_k+1)=f(k)[1-]=

=右式，　 ∴当n=k+1时，等式也成立。

综合①②，等式对于任意的nN^*都成立。