2005--2006学年度上学期期中考试高一试题
数 学
一、选择题(共12个小题,每小题5分,计60分)
1、在以下六个写法中①{0}∈{0,1,2} ②Φ![]() {0}
③{1,2,0}
{0}
③{1,2,0}![]() {1,2]} ④0∈Φ ⑤Φ
{1,2]} ④0∈Φ ⑤Φ![]() {Φ} ⑥Φ∈{Φ}错误写法的个数是
{Φ} ⑥Φ∈{Φ}错误写法的个数是
A、2 B、3 C、4 D、5
2、下列函数中,在指定区间上具有单调性的是
A、y=x2-3x,x∈R B、y=x2-3x,x∈(0,+∞)
C、y=∣x+2∣,x∈R D、y=∣x+2∣,x∈(0,+∞)
3、函数y=f(x)的图象与直线x=2的交点个数是
A、必有一个 B、至少有一个
C、至多有一个 D、有一个或两个
4、命题“若A ![]() B,则A=B”,与其逆命题、否命题、逆否命题中,真题的个数是
B,则A=B”,与其逆命题、否命题、逆否命题中,真题的个数是
A、0 B、2 C、3 D、4
5、已知命题p:x2-8x+12≠0,q:x-2≠0,则p是q的
A、充分不必要条件 B、必要不充分条件
C、充要条件 D、既不充分也不必要条件
6、函数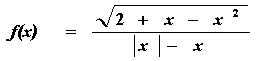 的定义域是
的定义域是
A、[-1,2] B、![]()
C、![]() D、
D、![]()
7、函数![]() 的反函数是
的反函数是
A、![]() B、
B、![]()
C、![]() D、
D、 ![]()
8、设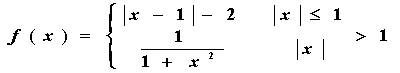 ,则
,则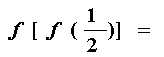
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
9、若函数f(x)满足f(-x)=f(x),且x>0时,f(x)=![]() ,则x<0时,f(x)等于
,则x<0时,f(x)等于
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
10、已知函数f(x)=ax2-2ax+b(a<0),则![]() 的大小关系是
的大小关系是
A、![]() B、
B、![]()
C、![]() D、
D、![]()
11、已知函数f(x)满足:f(p+q)=f(p)·f(q),f(1)=3,则 的值
的值
A、12 B、16 C、24 D、36
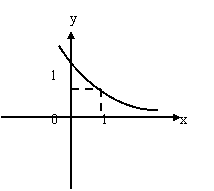 12、函数y=f(x-1)的图象如图所示,它在R上单调递减,现有如下结论:①f(0)>1
②f(
12、函数y=f(x-1)的图象如图所示,它在R上单调递减,现有如下结论:①f(0)>1
②f(![]() )<1 ③f-1(1)=0 ④ f-1(
)<1 ③f-1(1)=0 ④ f-1(![]() )>0,其中正确的个数
)>0,其中正确的个数
A、1 B、2 C、3 D、4
二、填空题(共4个小题,每小题4分,计16分)
13、含有三个实数的集合,既可表示为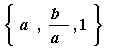 ,也可表示为
,也可表示为![]() ,则
,则![]() ___。
___。
14、函数![]() 定义域是(-∞,0),则a的取值范围是__。
定义域是(-∞,0),则a的取值范围是__。
15、函数y=x2-2x+3在闭区间[0,m]上有最大值3,最小值2,则m取值范围是______。
16、已知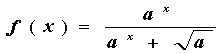 (其中a是大于0的常数),则
(其中a是大于0的常数),则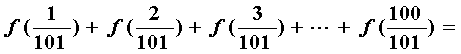 ___。
___。
三、解答题(共6个小题,计74分,要求写出文字说明,推理过程或演算步骤)
17、(12分)已知函数 的值域是{y∈R∣y≤0或y≥3},求此函数的定义域。
的值域是{y∈R∣y≤0或y≥3},求此函数的定义域。
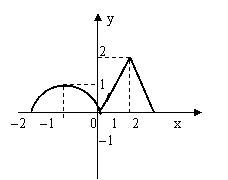
![]() 18、(12分)已知函数f(x)定义在[-2,2]上的图象如图所示,请分别画出如下函数的图象。
18、(12分)已知函数f(x)定义在[-2,2]上的图象如图所示,请分别画出如下函数的图象。
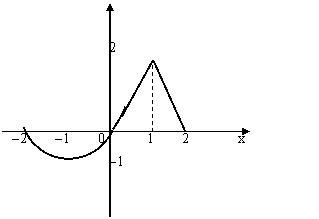
![]() (1)y=f(x+1)
(1)y=f(x+1)
![]() (2)y=f(-x)
(2)y=f(-x)
![]()
![]() (3)y=∣f(x)∣
(3)y=∣f(x)∣
(4)y=f(2x)
19、(12分)函数f(x)= -x3+ax在(0,1)上是增函数,求a的取值范围。
20、(12分)已知函数f(x)= ![]() ,且f-1(18)=a+2,g(x)=
,且f-1(18)=a+2,g(x)=![]() 的定义域是[0,1]。求:
的定义域是[0,1]。求:
(1)g(x)的解析式
(2)g(x)的单调区间
(3)g(x)的值域
21、有甲、乙两种商品,经营这两种商品所能获得的利润依次是P(万元)和Q(万元),它们与投入x(万元)的关系有经验公式:![]()
![]()
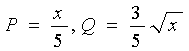 ,今有3万元资金投入经营甲、乙两种商品,为获得最大利润,则对甲、乙两种商品的资金投入分别是多少时,能获得最大的利润,获得的最大利润是多少?
,今有3万元资金投入经营甲、乙两种商品,为获得最大利润,则对甲、乙两种商品的资金投入分别是多少时,能获得最大的利润,获得的最大利润是多少?
22、(14分)时集合A={(x,y)∣a y2-x-1=0},
B={(x,y)∣4x2+2x-2y+5=0},C={(x,y)∣y=kx+b}.
(1)当a=0时,求A ∩ B
(2)当a=1时,问是否存在正整数k和b,使得(A∩C)∪(B∩C)=Φ ?若存在,求出k,b的值,若不存在,请说明理由。
参考答案:
一、 BDCBA CBBAB CC
二、13、-1 14、![]() 15、[1,2]
16、50
15、[1,2]
16、50
三、17、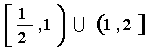
18、
 | |||||
 | |||||
 | |||||
19、a≥3
20、(1)![]()
(2)g(x)在[0,1]上是减函数,证明略。
(3)[-2,0]
21、设甲投入3-x万元,乙投入x万元,利润为y万元,则
![]() 当
当![]()
∴甲投入0.75万元,乙投入2.25万元,利润最大为1.05万元。
22、(1){(-1,3.5)}
(2)依题意,A ∩ B= Φ ,A ∩ C = Φ 即
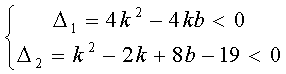 ,
,
∵k,b为正整数,
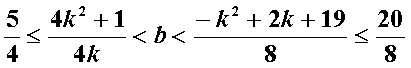
∴b=2,将b=2代回解得k=1 ∴存在b=2,k=1