2005年下学期高一数学期末考试试题

时量：120分钟　满分：150分

一、选择题：（本大题共10个小题，每小题5分，共50分）

1、已知全集，则集合的真子集共有

A、2个　　　　　　 B、3个　　　　　  C、4个　　　　　　 D、7个

2、集合，若非空，则实数的取值范围是

A、　　　　　  B、　　　　C、　　　　  D、

3、由命题p、q构成的“p或q”，“p且q”，“非p”形式的复合命题中，p或q为真，p且q为假，非p为真，那么

A、p真q假　　　　 B、p假q真　　　 C、p真q真　　　　 D、p假q假

4、有下列四个命题：

　  ①“若，则、互为倒数”的逆命题；

②“面积相等的三角形全等”的否命题；

③“若，则有实根”的逆否命题；

④“若，则”的逆否命题。其中真命题是

A、①②　　　　　  B、②③　　　　　  C、①②③　　　　　 D、③④

5、已知是命题，是A的否命题，如果，且，那么是的

A、充分不必要条件　　　　　　　　　　  B、必要不充分条件

C、充要条件　　　　　　　　　　　　　  D、既不充分又不必要条件

6、如图所示的图中可作为函数的图象的是

 　　　  A　　　　　　　　 B　　　　　　　　　 C　　　　　　　　　 D

7、已知函数在区间上是增函数，则实数的取值范围是

　  A、　　　　 B、　　　　　 C、　　　　　 D、

8、在各项都为正数的等比数列中，首项，前三项和为21，则

A、33　　　　　　 B、72　　　　　　  C、84　　　　　　  D、189

9、在等比数列中，，，则的值是

A、　　　　　　 B、　　　　　　 C、　　　　　　 D、

10、等差数列中，，且，是其前项和，则

A、都小于零，都大于零；

B、都小于零，都大于零；

C、都小于零，都大于零；

D、都大于零，都小于零。

二、填空题（本大题5个小题，每小题4分，共20分）

11、设函数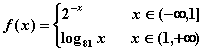，则满足的值为　　　　　　　 。

12、已知不等式的解集为，则的解集是　　　　　　　　　　　　　  。

13、某工厂现有现金200万元，由于技术创新使得每年资金比上一年增加10%，经过n年后该厂资金比现在至少翻一番，则n至少为　　　　　　　  。（lg2=0.301, lg1.1=0.041）

14、已知定义域为R的函数在上是增函数，满足且，则不等式的解集为　　　　　　　　　  。

15、设是首项为1的正项数列，且 ，它的通项公式是　　　　　　　　　  。

三、解答题（本大题共6个小题，共80分）

16、（满分12分）

　  已知，且，求实数的取值范围。

17、（满分12分）

是否存在实数，使“”是“”的充分条件？如果存在，求出的取值范围。是否存在实数，使“”是“”的必要条件？如果存在，求出的取值范围。

18、（满分14分）

已知等差数列中，，

（1）求数列的通项公式；

（2）若以数列中依次取出第2，4，8，…，项，按原来的顺序排成一个新数列，试求的前项和。

19、（满分14分）

某城市平均每天产生垃圾700吨，由甲、乙两厂进行处理，已知甲厂每小时可处理垃圾55吨，需费用550元；乙厂每小时可处理垃圾45吨，需费用495元。

（1）若该城市每天用于处理垃圾的费用不能超过7370元，问甲厂每天处理垃圾至少需要多少小时？

（2）若某天的垃圾甲厂处理了4小时，剩下的垃圾由乙厂处理，则该天的垃圾处理费用为多少？

20、（满分14分）

设的图象过，其反函数的图象过点

（1）求；

（2）记，求的最大值与最小值。

21、（满分14分）

数列中，且满足

（1）设，求；

（2）设，是否存在最大的整数，使得对任意，均有？若存在，求出的值；若不存在，说明理由。