算法
算法解题的一般思路，即算法分析（提炼问题的数学本质）——画出程序框图——按框图编写成程序语言——运行调试，改进程序。
总的来说，就是发现规律结合所掌握算法，通过模仿，操作，探索，寻找解决问题的通法。
一、满足方程的一组正整数称为勾股数或商高数，设计计算某一范围内的勾股数的算法．
例1．设计一个程序，求出不等式
的所有正整数解，并显示出来。
分析：因为相应函数
在
上是增函数。所以若有正整数
满足不等式，则所有小于的正整数也都是该不等式的解。
因此，我们可以设计一个算法，逐个检验1、2、3、……是否为该不等式的解，一直检验到第一个不满足该不等式的正整数
出现，则可以结束程序。因为根据函数的单调性，只要
，则
（
），
即大于或等于的正整数都不是的解。
⑴具体算法步骤：
第一步：初始化x=1
第二步：判断x是否为不等式的解。是则输出，并执行第三步；否则结束程序。
第三步：x=x+1,返回第二步。
⑵程序框图：
⑶程序：
二、用算法求任意平面图形的面积
以前我们在平面几何所遇到的面积、周长问题，都是在规则图形中根据给定的面积、周长公式求解。
实际上，当我们初步学习算法之后，我们可以结合无限分割的思想，自己编写程序来计算任意平面图形（包括规则及不规则图形）的面积、周长。
例2．设计算法求圆的面积。
⑴具体算法步骤如下：
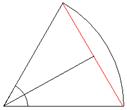第一步：将半径为
的圆分成
全等的扇形。
第二步：当正整数大到一定程度时，可以将扇形近似地
看成一个等腰三角形。顶角
可得该三角形底边上的高
所以扇形对应弦长
第三步：扇形的面积近似地看作三角形的面积
第四步：圆的面积为
⑵程序框图：
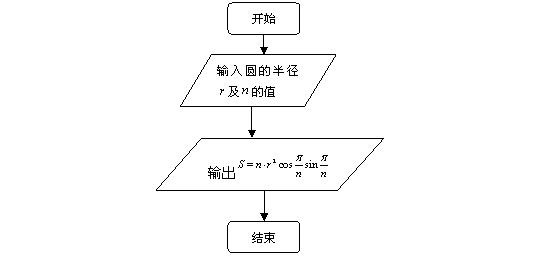
⑶程序：
例3．设计算法，求曲线
，直线
、
和轴围成的图形面积。
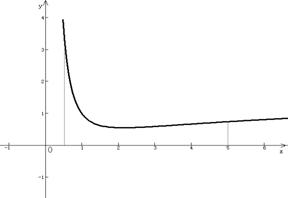分析：计算不规则图形的面积，
也可以利用无限分割的思
想来寻找算法。
首先将轴上0.5～5这段
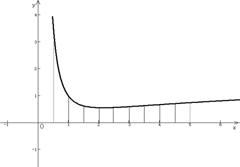
线段n等分，然后过每个
n等分点作垂直与轴的直
线，则将所求图形分为n个
近似于梯形的图形。
那我们就可以把所求图形面积看成是这n个梯形的面积之和。
⑴具体算法步骤如下：
第一步：输入正整数n。s=0
第二步：从左到右逐个计算这些
小梯形的面积，并逐个加到s。
第三步：输出s。
⑵程序框图：
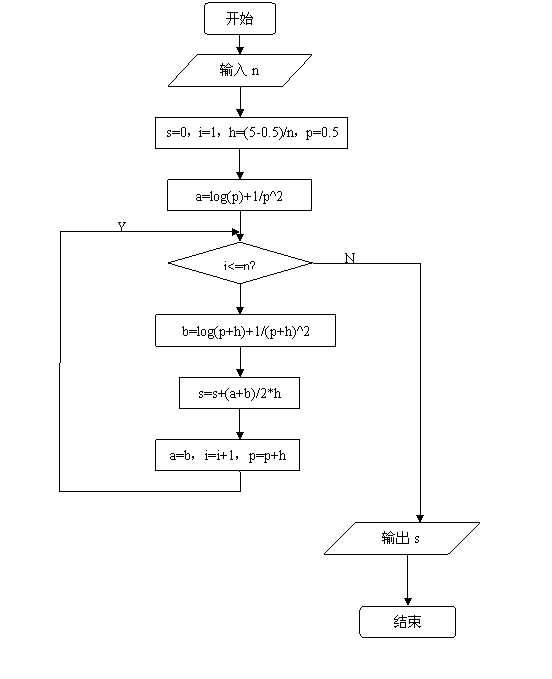
⑶程序：
三、算法在实际生活中的应用
例4．一辆邮车依次前往城市Ａ１，Ａ２，Ａ３，…Am（
），每到一个城市先卸下前面各城市发往该城市的邮袋1个，然后再装上该城市发往后面各城市的邮袋各1个，
设
ｎ是邮车从第ｎ个（1≤n＜m，n∈N* ）城市出发时邮车上邮袋的个数，设计一个算法，对任给两个正数ｍ＞ｎ，求ｎ.
分析:到达第n个城市时,邮袋个数为前一个城市的邮袋个数减去前面城市发往该市的n-1个邮袋，再加上发往后面各城市的（m-n）个邮袋，可用循环计算I从1至ｎ时，ｎ的变化。
⑴程序框图：
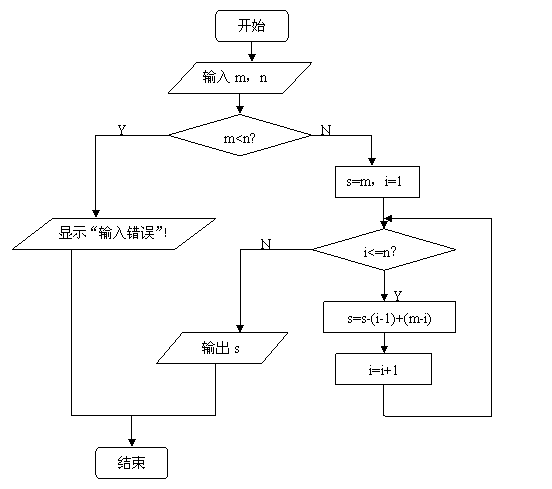
⑵程序：
随机事件的概率
例1、下面请同学们两人一组做一试验：每组抛掷硬币20次，并统计正、反面次数.统计每组正面向上次数如下：12，9，11，13，8，10，11，12，9，13，7，12，10，13，11，11，8，10，14，9，7，12，6，8，7.那么，在抛掷硬币试验中，出现正面的次数占总次数的百分比为多少呢？或者说，出现正面的频率为多少？
总试验次数为500次，出现正面的次数为253次，出现正面的频率为0.506.
请同学们来看这样一组数据：历史上曾有人作过抛掷硬币的大量重复试验，这便是试验结果.大家从这组数据中，是否可获得什么结论呢？
抛掷硬币试验结果表
| 抛掷次数(n) | 正面向上次数(频数m) | 频率( |
| 2048 4040 12000 24000 30000 72088 | 1061 2048 6019 12012 14984 36124 | 0.5181 0.5069 0.5016 0.5005 0.4996 0.5011 |
出现正面的频率值都接近于0.5.
再请同学们看这样两组数据，
某批乒乓球产品质量检验表
| 抽取球数n | 50 | 100 | 200 | 500 | 1000 | 2000 |
| 优等品数m | 45 | 92 | 194 | 470 | 954 | 1902 |
| 优等品频率 | 0.9 | 0.92 | 0.97 | 0.94 | 0.954 | 0.951 |
某种油菜籽在相同条件下的发芽试验结果表
| 每批粒数n | 2 | 5 | 10 | 70 | 130 | 310 | 700 | 1500 | 2000 | 3000 |
| 发芽粒数m | 2 | 4 | 9 | 60 | 116 | 282 | 639 | 1339 | 1806 | 2715 |
| 发芽频率 | 1 | 0.8 | 0.9 | 0.857 | 0.892 | 0.910 | 0.913 | 0.893 | 0.903 | 0.905 |
从表2可看到, 当抽查的球数很多时，抽到优等品的频率接近于0.95.
从表3可看到, 当试验的油菜籽的粒数很多时，油菜籽发芽的频率接近于0.9.
随机事件在一试验中是否发生虽然不能事先确定，但随着试验次数的不断增加，它的发生会呈现出一定的规律性，正如我们刚才看到的：某事件发生的频率在大量重复的试验中总是接近于某个常数.
一般地，在大量重复进行同一试验时，事件A发生的频率
总是接近于某个常数，在它附近摆动，这时就把这个常数叫做事件A的概率，记作P ( A ).
如上：记事件A为抛掷硬币时“正面向上”.
则P ( A ) = 0.5，即：抛掷一枚硬币出现“正面向上”的概率是0.5.
例2、若记事件A为抽取乒乓球试验中出现优等品，则P ( A ) = 0.95，即：任取一乒乓球得到优等品的概率是0.95.若记事件A：油菜籽发芽，则P ( A ) = 0.9, 即任取一油菜籽，发芽的概率为0.9.
概率这一常数从数量上反映了一个事件发生的可能性的大小.
如上：抛掷一枚硬币出现“正面向上”的可能性是50%；任取一乒乓球得到优等品的可能性是95%；任取一油菜籽，发芽的可能性是90%.
上述有关概率的定义，也就是求一个事件的概率的基本方法：进行大量的重复试验，用这个事件发生的频率近似地作为它的概率.
即：若记随机事件A在n次试验中发生了m次，则有0≤m≤n,0≤≤1.
于是可得：0 ≤ P ( A ) ≤1.
显然：（1）必然事件的概率是1，（2）不可能事件的概率是0.
例3、抛掷一个骰子，它落地时向上的数是3的倍数的概率是多少？
［分析］由于骰子落地时向上数可能有1，2，3，4，5，6六种情形，其中向上的数为3，6，这2种情形之一出现时，“向上的数是3的倍数”，这一事件（记作事件A）发生，因此事件A的发生包含的结果有2个.
解：记事件A为“向上的数是3的倍数”.
则事件A包含两个基本事件，即“向上的数是3”和“向上的数为6”.
且由题意得每一基本事件的概率均为
.
因此，事件A的概率为：P ( A ) = 
.
评述：如果某个事件A包含的结果有m个，那么事件A的概率P ( A )
= .
也可理解为：在一次试验中，等可能出现的n个结果组成一个集合I，这n个结果就是集合I的n个元素，各基本事件均对应于集合I的含有1个元素的子集，包含m个结果的事件A对应于I的含有m个元素的子集A.
因此从集合的角度看，事件A的概率是子集A的元素个数（记作card(A)）与集合I的元素个数（记作card（I））的比值，即：P ( A )
= 
如，上述骰子落地时向上的数是3的倍数，这一事件A的概率
P(A)= 
例4、.先后抛掷2枚均匀的硬币.
（1）一共可能出现多少种不同的结果？
（2）出现“1枚正面，1枚反面”的结果有多少种？
（3）出现“1枚正面，1枚反面”的概率是多少？
（4）有人说，“一共可能出现‘2枚正面’‘2枚反面’‘一枚正面，1枚反面’这3种结果，因此出现‘1枚正面，1枚反面’的概率是
.”这种说法对不对？
[分析] 由于是先后抛掷2枚均匀的硬币，所以在考查试验结果时，要分第一枚与第二枚不同的结果，然后再加以组合.
解：（1）由题意可知，可能出现的结果有：
“第1枚正面，第2枚正面”；
“第1枚正面，第2枚反面”；
“第1枚反面，第2枚正面”；
“第1枚反面，第2枚正面”.
即：一共可能出现“2枚正面”“2枚反面”“第1枚正面，第2枚反面”“第1枚反面，第2枚正面”四种不同的结果.
（2）由（1）得出现“1枚正面，1枚反面”的结果有“第1枚正面，第2枚反面”与“第1枚反面，第2枚反面”2种.
（3）由于此试验一共可能出现4种结果.而且每种结果出现的可能性是相等的，而出现“1枚正面，1枚反面”包含两种结果，所以其发生的概率为
，即
.
（4）这种说法不对，这是因为“1枚正面，1枚反面”这一事件由2个试验结果组成，这一事件发生的概率是而不是.
评述：要仔细分析试验的条件以及结果的出现类型.
例5、一个口袋内装有大小相等的1个白球和已编有不同号码的3个黑球，从中摸出2个球.
（1）共有多少种不同的结果？
（2）摸出2个黑球有多少种不同的结果？
（3）摸出2个黑球的概率是多少？
[分析]由题意可知袋中装有4个不同的球，从中任取2球的结果数即为从4个不同的元素中任取2元素的组合数；摸出2个黑球的结果数即为从3个不同的元素中任取2元素的组合数，且每种结果出现的可能性是相等的，即为等可能性事件.
解：（1）从装有4个球的口袋内摸出2个球，共有：C
=6种不同的结果，即由所有结果组成的集合I含有6个元素.
∴共有6种不同的结果.
（2）从3个黑球中摸出2个球，共有C
=3种不同的结果，这些结果组成I的一个含有3个元素的子集A，如图：
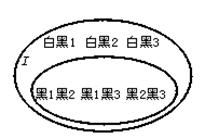
∴从口袋内摸出2个黑球有3种不同的结果.
（3）由于口袋内4个球的大小相等，从中摸出2个球的6种结果是等可能的，又在这6种结果中，摸出2个黑球的结果有3种，因此从中摸出2个黑球的概率
P ( A ) = 
. ∴ 从口袋内摸出2个黑球的概率是.
评述：仔细分析事件，灵活应用排列和组合知识解决问题.
例6、将骰子先后抛掷2次，计算：
（1）一共有多少种不同的结果？
（2）其中向上的数之和是5的结果有多少种？
（3）向上的数之和是5的概率是多少？
（学生讨论）
讨论1：将骰子抛掷1次，它落地时向上的数有1，2，3，4，5，6这6种结果，且每种结果出现的可能性是相等的.
讨论2：每次试验需分两步完成，且每步均会出现以上6种结果，每一次试验的结果为以上6种结果的任意组合，且每一组结果出现的可能性是相等的.
讨论3：向上的数和为5的结果，即出现1和4，2和3的组合的结果.
解：（1）将骰子抛掷1次，它落地时向上数有1，2，3，4，5，6这6种结果，根据分步计数原理，先后将这种玩具抛掷2次，一共有6×6=36种不同的结果.
（2）在上面所有结果中，向上的数之和为5的结果有（1，4），（2，3），（3，2），（4，1）4种，其中括弧内的前、后2个数分别为第1、2次抛掷后向上的数.
∴在2次抛掷中，向上的数之和为5的结果有4种.
以上结果可表示为：（其中不在线段上的各数为相应的2次抛掷后向上的数之和.）
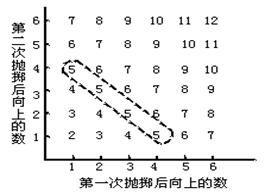
（3）由于骰子是均匀的，将它抛掷2次的所有36种结果是等可能出现的.
其中向上的数之和是5的结果（记为事件A）有4种，因此，P(A)=
.
∴抛掷骰子2次，向上的数之和为5的概率是
.
评述：注意分析事件的结果是否为有限的，且出现的可能性是否相等，即判断事件是否为等可能性事件，还要注意灵活应用排列和组合以及两原理的应用.
思考：在这个问题中，出现向上的数之和为5的倍数的概率是多少？
[分析]出现向上的数之和为5的倍数，即和为5或10.
其中和为5的结果有4种.
和为10的结果有（4，6），（6，4），（5，5）3种.
总之，出现向上的数之和为5的倍数的结果有7种.
因此，在这个问题中，出现向上的数之和为5的倍数的概率是
.
例7、. 随意安排甲、乙、丙3人在3天节日中值班，每人值班1天.
（1）这3人的值班顺序共有多少种不同的排列方法？
（2）其中甲在乙之前的排法有多少种？
（3）甲排在乙之前的概率是多少？
[分析]据题意可知，3人在3天节日中值班顺序数即为3个不同元素在3个不同位置上的排列数；其中甲在乙之前意味着甲、乙相邻且甲在乙之前，或甲、乙不相邻而甲在乙之前的排法.
解：（1）随意安排甲、乙、丙3人在3天节日中值班，每人值1天，则这3人的值班顺序共有6种不同的排列方法，即组成的集合I有6个元素.
∴这3人的值班顺序共有6种不同的排列方法.
（2）甲在乙之前的排法有：
甲乙丙，甲丙乙，丙甲乙3中不同的结果，这些结果组成I的一个含有3个元素的子集A.
如图所示：
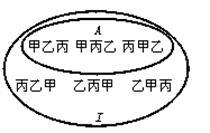
（3）由于是随意安排，即每人在每天值班的可能性是相等的，所以6种不同的值班顺序也是等可能的.又在这6种结果中，甲在乙之前的结果有3种，因此甲排在乙之前的概率为P(A)=.
∴甲排在乙之前的概率为.
例8. 在40根纤维中，有12根的长度超过30 mm, 从中任取一根，取到长度超过30 mm的纤维的概率是多少？
[分析]从40根纤维中，任取1根的结果数为40.由于其中12根长度超过30 mm，则抽到长度超过30 mm的结果数为12.
解：从40根纤维中任取1根，共有40种不同的结果，且每种结果是等可能的.由于其中12根长度超过30 mm, 则抽到长度超过30 mm的纤维，共有12种不同的结果.
∴取到长度超过30 mm的纤维的概率为
.