三角函数测试题（一）
一、选择题（每小题5分，共60分，请将所选答案填在括号内）
1．下列等式中成立的是 （ ）
A．sin（2×360°－40°）=sin40° B．cos（3π+
）=cos
C．cos370°=cos（－350°） D．cos
π=cos（－
π）
2．若
的终边所在象限是 （ ）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
3．若
，则
等于
（ ）
A． cosθ－sinθ B．sinθ+cosθ C．sinθ－cosθ D．－cosθ－sinθ
4．y =
的值域是 （ ）
A．{1,－1} B． {－1,1,3} C． {－1,3} D．{1,3}
5．已知锐角
终边上一点的坐标为（
则= （ ）
A．
B．3 C．3－
D．
－3
6．将角的终边顺时针旋转90°，则它与单位圆的交点坐标是 （ ）
A．（cos,sin） B．（cos,－sin） C．(sin, －cos) D．(sin, cos)
7．若是第三象限角，则下列四个三角函数式中一定为正数的是 （ ）
A．sin+cos B．tan+sin C．sin·sec D．cot·sec
8．
（ ）
A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件
9．已知是三角形的一个内角，且
，那么这个三角形的形状为（ ）
A．锐角三角形 B．钝角三角形 C．不等腰直角三角形 D．等腰直角三角形
10.若f(cosx)=cos2x，则f(sin15°)的值等于 （ ）
A．
B．－
C．－
D．
11．若
是第一象限角，则
中能确定为正值的有（ ） A．0个 B．1个 C．2个
D．2个以上
12．若函数
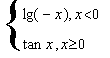,则
（ ）
A．
B．- C．2 D．-2
第Ⅱ卷（非选择题，共90分）
二、填空题（每小题4分，共16分，请将答案填在横线上）
13．已知
则
.
14．函数y=tan（x－
）的定义域是
.
15．已知
，则
=___
__.
16．已知角的终边上的点P与A(a，b)关于x轴对称（a≠0且b≠0），角β的终边上的点Q与A关于直线y=x对称，则sin·secβ+tan·cotβ+sec·cscβ= ．
三、解答题（本大题共74分）
17．（8分）若β∈［0，2π］，且
=sinβ－cosβ，求β的取值范围．
18．（12分）在ΔABC中，角A、B、C所对的边分别为a、b、c，且
.
（Ⅰ）求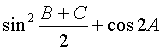
的值；（Ⅱ）若
，求b·c的最大值.
19．（12分）（1）已知角的终边在直线y=－3x上，求10sin+3sec的值．
（2）已知关于x的方程
的两根相等，且
为锐角，求的值。
20．（15分）化简：（1）
．
（2）tan1°tan2°tan3°···tan88°tan89°
（3）
21．（12分）（1）已知sinθ+cosθ=
，θ∈(0，π)，求cotθ的值.
（2）设cosθ
(m>n>0),求θ的其他三角函数值。
22．（15分） 证明：（1）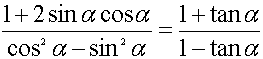
（2）
（3）
三角函数测试题（一）参考答案
一、选择题
1．C 2．D3．A4．C 5．C 6．C7．C 8．A9．B 10．C 11．C12．C
二、填空题13．
14．{xx≠
π+kπ,k∈Z} 15．
16．0
三、解答题 17．解析：∵
=
=sinβ+cosβ=sinβ－cosβ
∴sinβ≥0，cosβ≤0 ∴β是第二象限角或终边在x轴负半轴和y轴正半轴上的角
∵0≤β≤2π，∴
≤β≤π.
18． 解析: (Ⅰ)
=
=
=
= 
(Ⅱ) ∵
∴
,
又∵
∴
当且仅当 b=c=
时,bc=
,故bc的最大值是.
19．（1）解析：设P（m，－3m）是θ终边上任一点，则r=
m
当m＞0时，r=
m. ∴sinθ=
， secθ=
∴10sinθ+3secθ=－3
=0 当m＜0时，r=－m，
∴sinθ=
，secθ=
∴10sinθ+3secθ=3
=0
综上，得10sinθ+3secθ=0 （2）（略）
20．（1）解析：原式=
·
=
=
=tanx
（2）．解析：∵sinθ+cosθ=
，(1)将其平方得，1+2sinθcosθ=
，
∴2sinθcosθ=－
，∵θ∈(0，π)， ∴cosθ＜0＜sinθ
∵(sinθ－cosθ)2=1－2sinθcosθ=
， ∴sinθ－cosθ=
(2)
由（1）（2）得sinθ=
，cosθ=－
，∴cotθ=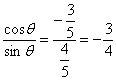
（3）．解析：设直角三角形的两个锐角分别为α、β，则可得α+β=，∴cosα=sinβ
∵方程4x2－2(m+1)x+m=0中，Δ=4（m+1）2－4·4m=4(m－1)2≥0 ∴当m∈R，方程恒有两实根.
又∵cosα+cosβ=sinβ+cosβ=
，cosα·cosβ=sinβcosβ=
∴由以上两式及sin2β+cos2β=1，得1+2·=()2 解得m=±
当m=时，cosα+cosβ=
＞0，cosα·cosβ=
＞0，满足题意，
当m=－时，cosα+cosβ=
＜0，这与α、β是锐角矛盾，应舍去. 综上，m=
21．（略）
22．（略）