2005－2006学年度上学期
集合与集合的运算
说明：本试卷分第I卷和第II卷两部分，第I卷60分，第II卷90分，共150分；答题时间150分钟．
第Ⅰ卷（共60分）
一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的．
1．若集合
当中的元素是△ABC的三边长，则该三角形是 （ ）
A．正三角形 B．等腰三角形 C．不等边三角形 D．等腰直角三角形
2．集合{1，2，3}的真子集共有 （ ）
A．5个 B．6个 C．7个 D．8个
3．设A、B是全集U的两个子集，且A
B，则下列式子成立的是 （ ）
A．CUACUB B．CUA
CUB=U C．A
CUB=
D．CUAB=
4．如果集合A={xax2＋2x＋1=0}中只有一个元素，那么a的值是 （ ）
A．0 B．0 或1 C．1 D．不能确定
5．设集合
，
其中
，则下列关系中正确的是（ ）
A．
M B．
C．
D．
6．已知A={1，2，a2-3a-1},B={1,3},A
{3,1}则a等于 （ ）
A．-4或1 B．-1或4 C．-1 D．4
7． 设S、T是两个非空集合，且S
T，TS，令X=S
那么SX= （ ）
A．X B． T C． D．S
8．给定集合
，定义 
．若 
，
则集合 
中的所有元素之和为 （ ）
A．15 B．14 C．27 D．-14
9．设集合M={xx∈Z且－10≤x≤－3}，N={xx∈Z且x≤5 }，则M∪N中元素的个 数为 （ ）A．11 B．10 C．16 D．15
10．设U={1，2，3，4，5}，A，B为U的子集，若AB={2}，（CUA）B={4}，
（CUA）（CUB）={1，5}，则下列结论正确的是 （ ）
A．3
B．3
C．3
D．3
11．设A={x
},B={x
},若AB={2,3,5},A、B分别
为 （ ）
A．{3，5}、{2，3} B．{2，3}、{3，5}
C．{2，5}、{3，5} D．{3，5}、{2，5}
12．设※是集合A中元素的一种运算, 如果对于任意的x、y
, 都有x※y, 则称运算※对集合A是封闭的, 若M
则对集合M不封闭的运算是
（ ）
A．加法 B．减法 C．乘法 D．除法
第Ⅱ卷（共90分）
二、填空题：本题共4小题，每小题4分，共16分．把答案填在题中的横线上．
13．已知集合A={0，2，3}，B={
}，则B的子集的个数是 ．
14．若一数集中的任一元素的倒数仍在该集合中，则称该集合为“可倒数集”，试写出一个含三个元素的可倒数集_________．（只需写出一个集合）
15． 定义集合A和B的运算：
． 试写出含有集合运算符号“
”、“
”、“
”，并对任意集合A和B都成立的一个等式：_______________．
16．设全集为，用集合A、B、C的交、并、补集符号表图中的阴影部分．
（1） （2）
 |
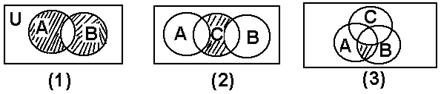（3）
三、解答题:本大题共6小题，共74分．解答应写出必要的文字说明、证明过程及演算步骤．
17． 已知集合A={x1≤x＜4＝，B={xx＜a＝, 若A
B，试求实数a的取值集合．（12分）
18． 设A={x
,其中x
R,如果AB=B，求实数a的取值范围． （12分）
19．设全集U={x
},集合A={x
},B={
x2+px+12=0},
且（CUA）B={1，4，3，5}，求实数P、q的值．（12分）
20．集合A={（x,y）
},集合B={（x,y）
,且0
}，又A
，求实数m的取值范围．（12分）
21．集合A＝｛x｜x2－ax＋a2－19＝0｝，B＝｛x｜x2－5x＋6＝0｝．若A∩B＝A∪B，求a的值．（12分）
22．知集合
,
，
是否存在正实数，使得
，如果存在求的集合？如果不存在请说明理由． （14分）
|
2005－2006学年度上学期
高中学生学科素质训练
高一数学同步测试（1）—集合与集合的运算答案
一、选择题
1．C 2．D 3．C 4．B 5．C 6．B 7．D 8．A 9．C 10．C 11．A 12．D
二、填空题
13． 16．
14． 
．
15．
；
；
；…．
16．（1）（AB）
（2）[（CUA）（CUB）]
；
（3）（AB）（CUC）．
三、解答题
17． 将数集A表示在数轴上(如图)，要满足AB，表示数a的点必须在4或4的右边，所求a的取值集合为{aa≥4}．
18． A={0，-4}，又AB=B，所以BA．
（i）B=时，
4（a+1）2-4(a2-1)<0，得a<-1；
(ii)B={0}或B={-4}时，0 得a=-1；
（iii）B={0，-4}，
解得a=1．
综上所述实数a=1 或a
-1．
19． U={1，2，3，4，5} A={1，4}或A={2，3}
CuA={2,3,5}或{1，4，5} B={3，4}（CUA）B=（1，3，4，5），又
B={3，4} 
CUA={1，4，5} 故A只有等于集合{2，3}，P=-（3+4）=-7 ， q=2×3=6．
20． 由AB
知方程组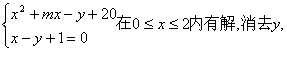
得x2+(m-1)x=0 在0x
内有解，
即m
3或m-1。
若3，则x1+x2=1-m<0,x1x2=1,所以方程只有负根。
若m-1,x1+x2=1-m>0,x1x2=1,所以方程有两正根，且两根均为1或两根一个大于1，一个小于1，即至少有一根在[0，2]内。
因此{m
<m-1}．
21．由已知，得B＝｛2，3｝．
∵A∩B＝A∪B，∴A＝B．于是2，3是一元二次方程x2－ax＋a2－19＝0的两个根，由韦达定理知：
解之，得 a＝5．
22．∵
， ∴
，
将
代入
，得
，
设
，
令
，
当
时， 
．
依题意得
， ∴
，
∴适合条件的存在其集合为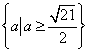
．