高一数学《三角函数》第一单元练习题
一、选择题
1.使sinx·cosx<0成立的角α的集合可表示为 ( )
A.{a|2kπ+![]() <α<2kπ+π,k∈Z
<α<2kπ+π,k∈Z![]() B.{α|kπ+
B.{α|kπ+![]() <α<kπ+π,k∈Z
<α<kπ+π,k∈Z![]()
C.{α|2kπ+![]() <α<2kπ+2π,k∈Z
<α<2kπ+2π,k∈Z![]() D.{α|kπ<α<kπ+
D.{α|kπ<α<kπ+![]() ,k∈Z}
,k∈Z}
2. 若cosa·tana<0且sina·tana>0, 则a的终边在 ( )
A.第一象限 B. 第二象限 C. 第三象限 D. 第四象限
3.已知
![]() 是第三象限角,且
是第三象限角,且![]() ,则( )
,则( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.和![]() 的角终边相同的角的集合是( )
的角终边相同的角的集合是( )
A.![]() B.
B.![]()
C.![]() D.
D. ![]()
5.如果角α的顶点在原点,始边在x轴的正半轴上,终边在函数y=-5x (x<0)的图象上,那么cosα的值为 ( )
A.±![]() B.
B. ![]() C.-
C.-![]() D.-
D.-![]()
6.若![]() ,则
,则![]() 的值为( )
的值为( )
A.-4 B.4 C.-8 D.8
7.若![]() ,则
,则![]() 的值等于 (
)
的值等于 (
)
A.0 B.1 C.2 D. 3
8.若![]() ,则
,则![]() 的值为(
)
的值为(
)
A.0 B.1 C.-1 D.±1
9. ![]() 、
、![]() 、
、![]() 的大小关系为 ( )
的大小关系为 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
10、下列结论成立的是( )
A、![]() 且
且![]() B、
B、![]() 且
且![]()
C、![]() 且
且![]() D、
D、![]() 且
且![]()
二、填空题
11.设θ∈(0,2π),若P (sinθ,tanθ)点在第三象限,则θ的取值范围是 .
12.已知f (n)=sin![]() (n∈N+),则f (1) + f (2 ) + … + f (2004 ) 的值等于
.
(n∈N+),则f (1) + f (2 ) + … + f (2004 ) 的值等于
.
13.若角![]() 的终边过点
的终边过点![]() ,且
,且![]() ,则
,则![]() .
.
14.若α是第三象限角,则 ①sinα+cosα<0
②tanα-sinα>0 ③![]() ④sinα+tanα>0中正确的是
.
④sinα+tanα>0中正确的是
.
15.函数![]() 的值域为__________.
的值域为__________.
16.函数![]() 的定义域是 。
的定义域是 。
17.设tanx=1,则角x的解集是 。
18.若![]() ,则
,则![]() 。
。
三、解答题
19.已知角
![]() 的终边上一点
的终边上一点![]()
![]() ,求角
,求角 ![]() 的三个三角函数值.
的三个三角函数值.
20.已知角
![]() 终边上一点
终边上一点![]() ,且
,且![]() ,求
,求 ![]() 和
和 ![]() 之值.
之值.
21.已知扇形的周长为30,当它的半径R和圆心角![]() 各取何值时,扇形的面积最大?并求出扇形面积的最大值。
各取何值时,扇形的面积最大?并求出扇形面积的最大值。
22.已知![]() ,求下列各式的值:
,求下列各式的值:
(1)![]() (2)
(2)![]()
(3)![]() (4)
(4)![]()
23.已知 ![]() ,求证:
,求证:![]()
24.求证:![]()
25.已知![]() ,求
,求![]() 、
、![]() 的值。
的值。
26.已知![]() 是第三象限角,化简
是第三象限角,化简![]() 。
。
27.已知![]() ,而
,而![]() 、
、![]() 是方程
是方程![]() 的两实数根,求
的两实数根,求![]() 和
和![]() 的值。
的值。
28.已知![]() ,
,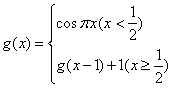 ,求
,求
![]() 的值。
的值。
