高一数学《平面向量》检测题

一、选择题（本大题共12小题，每小题5分，共60分）

１、下列关系式正确的是（　　）

Ａ、　　Ｂ、是一个向量　　Ｃ、　　Ｄ、

２、在△中，、、分别是ＡＢ、ＢＣ、ＣＡ边的中点，则（　　）

Ａ、　　　　Ｂ、　　　　Ｃ、　　　　Ｄ、

３、已知点关于点的对称点是，则点到原点的距离是（　　）

Ａ、　　　　Ｂ、　　　　　Ｃ、　　　　　Ｄ、

４、已知，，则等于（　　）

Ａ、２３　　　　Ｂ、５７　　　　　Ｃ、６３　　　　　　Ｄ、８３

５、已知，，且与的夹角为钝角，则的取值范围是（　　）

Ａ、　　　　Ｂ、　　　　Ｃ、　　　　Ｄ、

６、已知均为单位向量，且夹角为，那么等于（　　）

Ａ、　　　　　Ｂ、　　　　　Ｃ、　　　　　　Ｄ、

７、已知，则向量在向量方向上的投影为（　　）

Ａ、　　　　Ｂ、　　　　　Ｃ、　　　　　　Ｄ、

8、化简以下各式：①；②；③；

④，结果为零向量的个数是（　　）

Ａ、1　　　　Ｂ、2　　　　　Ｃ、3　　　　Ｄ、4

9、若⊥，则与的夹角是（　　）

Ａ、　　　　Ｂ、　　　　　Ｃ、　　　　　Ｄ、

10、下列各向量组中，能作为表示它们所在平面内所有向量的一组基底的是（　　）

Ａ、　　　　　Ｂ、

Ｃ、　　　　　Ｄ、

11、已知，若与平行，则等于（　　）

Ａ、　　　　　Ｂ、　　　　　Ｃ、　　　　　　Ｄ、

12、已知点，，点在坐标轴上，∠，则满足条件的点个数为（　　）

Ａ、１　　　　Ｂ、２　　　　　Ｃ、３　　　　　Ｄ、４

二、填空题（本大题共4小题，每小题5分，共20分）

13、已知，且与共线，，则　　　　　。

14、已知，则　　　　　　。

15、设点，Ｐ是直线ＡＢ上的一点，且，则点Ｐ的坐标是　　　　　　　　　。

16、在△中，有命题：①；②；

③若，则△是等腰三角形；④，则△　为锐角三角形。上述命题正确的是　　　　　　　　。（写出所有正确命题的序号）

三、解答题（本大题共6小题，共70分）

17、已知，若⊥，∥，求及与的夹角。（10分）

18、设，是平面直角坐标系中x轴和y轴方向上的单位向量，，， ，求四边形ABCD的面积。（12分）

19、平面内有向量，，，点为直线上的一个动点，当取最小值时，求的坐标和∠的余弦值。（12分）

20、已知，求点的轨迹方程。（12分）

21、已知，且存在实数和，使得，，并且⊥，试求的最小值。（12分）

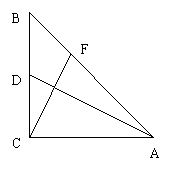22、如图，在等腰直角三角形中，∠是直角，，是的中点，是上的一点，且。求证：⊥。（12分）