高一下学期期末考试复习题
一、选择题: (本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1. 如果a>b>c,a+b+c=0,则有 ( )
(A)a·b>a·c (B)a·c>b·c (C)a·b>c·b (D) a2>b2>c2
2.
已知![]() ,则下列不等式中正确的是
(
)
,则下列不等式中正确的是
(
)
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
3.
如果![]() ,
,![]() 不共线,则下列四组向量共线的有
( )
不共线,则下列四组向量共线的有
( )
⑴2![]() ,-2
,-2![]() ; ⑵
; ⑵![]() -
-![]() ,-2
,-2![]() +2
+2![]() ; ⑶4
; ⑶4![]() -
-![]()
![]() ,
,![]() -
-![]()
![]() ; ⑷
; ⑷![]() +
+![]() ,2
,2![]() -2
-2![]()
(A)⑵⑶ (B) ⑵⑶⑷ (C) ⑴⑶⑷ (D)⑴⑵⑶⑷
4.
如果四边形ABCD是菱形,点P在对角线AC上(不含端点),则![]() =
( )
=
( )
(A)![]() (
(![]() +
+![]() ) ,
) , ![]() ∈(0,1) (B)
∈(0,1) (B) ![]() (
(![]() +
+![]() ) ,
) , ![]() ∈(0,
∈(0,![]() )
)
(C)![]() (
(![]() -
-![]() ) ,
) , ![]() ∈(0,1) (D)
∈(0,1) (D) ![]() (
(![]() -
-![]() ) ,
) , ![]() ∈(0,
∈(0,![]() )
)
5.
如果A、B、C三点共线,并且A、B、C的纵坐标分别为2,5,10,则点A分![]() 的比为
( )
的比为
( )
(A)![]() (B)
(B)![]() (C)-
(C)-![]() (D) -
(D) -![]()
6. △ABC中,若(a-c·cosB)sinB=(b-c·cosA)sinA,则这个三角形是 ( )
(A)底角不为45![]() 的等腰△ (B) 锐角不为45
的等腰△ (B) 锐角不为45![]() 的直角△
(C)等腰直角△ (D) 等腰或者直角△
的直角△
(C)等腰直角△ (D) 等腰或者直角△
7. △ABC中,“A=B”是“sinA=sinB”的( )(A)充分不必要条件 (B) 必要不充分条件 (C)充要条件 (D) 非充分非必要条件
8. 函数y=2sin2x+sin2x是 ( )
A.以2π为周期的奇函数 B.以2π为周期的非奇非偶函数
C.以π为周期的奇函数 D.以π为周期的非奇非偶函数
9. 将函数![]() 的图象向右平移
的图象向右平移![]() 个单位后再作关于
个单位后再作关于![]() 轴对称的曲线,得到函数
轴对称的曲线,得到函数![]() 的图象,则
的图象,则![]() 的表达式是
( ) (A)
的表达式是
( ) (A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
10. 给出四个函数,则同时具有以下两个性质的函数是:①最小正周期是![]() ;②图象关于点(
;②图象关于点(![]() ,0)对称
( ) (A)
,0)对称
( ) (A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
11. 已知函数y=2sin(ωx)在[-![]() ,
,![]() ]上单调递增,则实数ω的取值范围是
( )
]上单调递增,则实数ω的取值范围是
( )
A.(0,![]()
![]() B.(0,2
B.(0,2![]() C.(0,1
C.(0,1![]() D.
D.
![]()
12. 已知函数![]() (x∈R),设当y取得最大值时,角x的值为
(x∈R),设当y取得最大值时,角x的值为![]() ,当y取得最小值时,角x的值为
,当y取得最小值时,角x的值为![]() ,其中
,其中![]() 、
、![]() 均属于区间
均属于区间![]() ,则
,则![]() 的值为
(
)
的值为
(
)
A、![]() B、
B、![]() C、0
D、
C、0
D、![]()
二、填空题: (本大题共4个小题,每小题4分,共16分,把答案填在题中横线上)
13. 如果向量![]() 、
、![]() 夹角120
夹角120![]() ,并且
,并且![]() =2,
=2,![]() =5,则(2
=5,则(2![]() -
-![]() )·
)·![]() =
.
=
.
14.
已知0<α<![]() ,tan
,tan![]() +cot
+cot![]() =
=![]() ,则sin(
,则sin(![]() )的值为
)的值为
15. 设一个三角形三边长分别为x、y,![]() ,则最长边与最短边的夹角为
;
,则最长边与最短边的夹角为
;
16. 已知一个不等式①![]() ,②
,②![]() ,③
,③![]() ,以其中的两个作条件,余下的一个作结论,则可组成____________个正确命题。
,以其中的两个作条件,余下的一个作结论,则可组成____________个正确命题。
三、解答题: (本大题共6小题, 共74分, 解答应写出文字说明、证明过程或演算步骤)
17. 如果4![]() -2
-2![]() =(-2,2
=(-2,2![]() ),
),![]() =(1,
=(1,![]() ),
),![]() ·
·![]() =3,
=3,![]() =4,求
=4,求![]() 、
、![]() 夹角。
夹角。
18.  某单位用木料制作如图所示的框架, 框架的下部是边长分别为x、y(单位:m)的矩形.上部是等腰直角三角形. 要求框架围成的总面积8cm2. 问x、y分别为多少(精确到0.001m) 时用料最省?
某单位用木料制作如图所示的框架, 框架的下部是边长分别为x、y(单位:m)的矩形.上部是等腰直角三角形. 要求框架围成的总面积8cm2. 问x、y分别为多少(精确到0.001m) 时用料最省?
19.
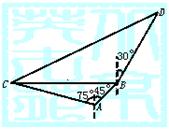 在海岸A处,发现北偏东45°方向,距离A为(
在海岸A处,发现北偏东45°方向,距离A为(![]() -1)海里的B处有一艘走私船,在A处北偏西75°方向距离A为2海里的C处有我方一艘辑私艇奉命以10
-1)海里的B处有一艘走私船,在A处北偏西75°方向距离A为2海里的C处有我方一艘辑私艇奉命以10![]() 海里/小时的速度追截走私船,此时走私船正以10海里/小时的速度从B处向北偏东30°方向逃窜,问辑私艇沿什么方向,才能最快追上走私船?需要多长时间?
海里/小时的速度追截走私船,此时走私船正以10海里/小时的速度从B处向北偏东30°方向逃窜,问辑私艇沿什么方向,才能最快追上走私船?需要多长时间?
20.
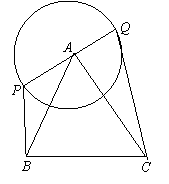
△ABC中,BC=3![]() ,AC=4,AB=2
,AC=4,AB=2![]() ,PQ是以A为圆心,以
,PQ是以A为圆心,以![]() 为半径的圆的直径,求
为半径的圆的直径,求![]() 的最大值与最小值,并且指出取得最值时
的最大值与最小值,并且指出取得最值时![]() 的方向。
的方向。
21.
已知函数f(x)=Asinωx+Bcosωx(其中A,B,ω为实常数,且ω>0)的最小正周期为2,并且当x=![]() 时,f(x)的最大值为2.
时,f(x)的最大值为2.
(1) 函数f(x)的表达式;
(2) 在区间[![]() ]上函数f(x)存在对称轴,求此对称轴方程。
]上函数f(x)存在对称轴,求此对称轴方程。
22.已知![]() 的三个内角
的三个内角![]() 成等差数列,设
成等差数列,设![]() ,
,![]()
(1) 试求![]() 的解析式及其定义域;
的解析式及其定义域;
(2) 判断其单调性并加以证明;
(3) 求这个函数的值域。
数学参考答案
一、选择题:
ACAAC DCDBD AB
二、填空题:
13.
13; 14. ![]() ; 15.
; 15. ![]() ; 16. 3
; 16. 3
三、解答题:
17. 解: (4![]() -2
-2![]() )·
)·![]() =(-2,2
=(-2,2![]() )·(1,
)·(1,![]() )=-2+6=4, 故
)=-2+6=4, 故![]() ·
·![]() =4, cos<
=4, cos<![]() ,
, ![]() >=
>=![]() .
.
所以![]() 、
、![]() 的夹角为
的夹角为![]() .
.
18. 解: 由题意得 xy+![]() x2=8,∴y=
x2=8,∴y=![]() =
=![]() (0<x<4
(0<x<4![]() ).
).
于定, 框架用料长度为 l=2x+2y+2(![]() )=(
)=(![]() +
+![]() )x+
)x+![]() ≥4
≥4![]() .
.
当(![]() +
+![]() )x=
)x=![]() ,即x=8-4
,即x=8-4![]() 时等号成立.
时等号成立.
此时, x≈2.343,y=2![]() ≈2.828.
≈2.828.
19.解: 设需要t小时追上走私船.
∵BC2=AC2+AB2-2AC·ABcosCAB
=22+(![]() -1)2-2×2×(
-1)2-2×2×(![]() -1)cos120°=6,
-1)cos120°=6,
∴BC=![]() ,
,
在△CBD中,∠CBD=120°
cosCBD=![]()
整理,得100t2-5![]() t-3=0 ,解得t=
t-3=0 ,解得t=![]() 或t=-
或t=-![]() (舍去)
(舍去)
又∵![]() ,即:
,即:![]()
解得∠DCB=30°
答:沿北偏东60°追击,需![]() 小时
小时
20. 解: ![]() =(
=(![]() +
+![]() )(
)(![]() +
+![]() )=3+
)=3+![]() ·
·![]() +
+![]() ·
·![]() =3+
=3+![]() (
(![]() -
-![]() )=3+
)=3+![]() ·
·![]() =3+6cos<
=3+6cos<![]() ,
, ![]() >
>
(1) <![]() ,
, ![]() >=0时,
>=0时, ![]() 的最大值为9;
的最大值为9;
(2) <![]() ,
, ![]() >=
>=![]() 时,
时, ![]() 的最小值为-3.
的最小值为-3.
21.解: (1) ![]() =
= ![]() .
.
![]() =2,
=2, ![]() A+
A+![]() B=2, 解得A=
B=2, 解得A=![]() , B=1
, B=1
f(x)=2sin(![]() x+
x+![]() )
)
(2) 由![]() x+
x+![]() =k
=k![]() +
+![]() ,
,
解得x=k+![]() , k
, k![]() Z及x
Z及x![]() [
[![]() ]
]
得到k=4.
故对称轴方程为x=4![]()
22. 解: (1) 2B=A+C=![]() -B, ∴ B=
-B, ∴ B=![]()
f(x)=cos![]() ·
·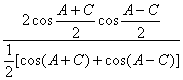 =
=![]() ,
,
由-![]() <
<![]() <
<![]() , 得
, 得![]() <cos
<cos![]() ≤1
≤1
∴x![]() (
(![]() ,
, ![]() )(
)(![]() , 1
, 1![]() .
.
(2) 据定义不能证明f(x)在(![]() ,
, ![]() )、(
)、(![]() , 1
, 1![]() 上均单调递减.
上均单调递减.
(3) 由(2)得y![]() (-
(-![]() , -1)
, -1)![]() [2, +
[2, +![]()
![]() .
.